4.4 Batallas entre paradigmas

En esta seccion compararemos los tres paradigmas de computabilidad efectiva que hemos desarrollado anteriormente. Para esto probaremos que cada uno de dichos paradigmas "vence" al otro en el sentido que incluye por lo menos todas las funciones que incluye el otro en su modelizacion del concepto de funcion \(\Sigma\)-efectivamente computable.

4.4.1 Neumann vence a Godel

Usando macros podemos ahora probar que el paradigma imperativo de Neumann es por lo menos tan abarcativo como el funcional de Godel. Mas concretamente:

Proof. Probaremos por induccion en \(k\) que

Si \(h\in\mathrm{R}_{k}^{\Sigma}\), entonces \(h\) es \(\Sigma\)-computable.

El caso \(k=0\) es dejado al lector. Supongamos (*) vale para \(k\), veremos que vale para \(k+1\). Sea \(h\in\mathrm{R}_{k+1}^{\Sigma}-\mathrm{R}_{k}^{\Sigma}.\) Hay varios casos

Caso 1. Supongamos \(h=M(P)\), con \(P:\omega\times\omega^{n}\times\Sigma^{\ast m}\rightarrow\omega\), un predicado perteneciente a \(\mathrm{R}_{k}^{\Sigma}\). Por hipotesis inductiva, \(P\) es \(\Sigma\)-computable y por lo tanto tenemos un macro \[\left[\mathrm{IF}\;P(\mathrm{V}1,...,\mathrm{V}\overline{n+1},\mathrm{W}1,...,\mathrm{W}\bar{m})\;\mathrm{GOTO}\;\mathrm{A}1\right]\] lo cual nos permite realizar el siguiente programa \[\begin{array}{ll} \mathrm{L}2 & \left[\mathrm{IF}\;P(\mathrm{N}\overline{n+1},\mathrm{N}1,...,\mathrm{N}\bar{n},\mathrm{P}1,...,\mathrm{P}\bar{m})\;\mathrm{GOTO}\;\mathrm{L}1\right]\\ & \mathrm{N}\overline{n+1}\leftarrow\mathrm{N}\overline{n+1}+1\\ & \mathrm{GOTO}\;\mathrm{L}2\\ \mathrm{L}1 & \mathrm{N}1\leftarrow\mathrm{N}\overline{n+1} \end{array}\] Es facil chequear que este programa computa \(h.\)

Caso 2. Supongamos \(h=R(f,\mathcal{G})\), con \[\begin{aligned} f & :S_{1}\times...\times S_{n}\times L_{1}\times...\times L_{m}\rightarrow\Sigma^{\ast}\\ \mathcal{G}_{a} & :S_{1}\times...\times S_{n}\times L_{1}\times...\times L_{m}\times\Sigma^{\ast}\times\Sigma^{\ast}\rightarrow\Sigma^{\ast}\text{, }a\in\Sigma \end{aligned}\] elementos de \(\mathrm{R}_{k}^{\Sigma}\). Sea \(\Sigma=\{a_{1},...,a_{r}\}.\) Por hipotesis inductiva, las funciones \(f\), \(\mathcal{G}_{a}\), \(a\in\Sigma\), son \(\Sigma\)-computables y por lo tanto podemos hacer el siguiente programa via el uso de macros \[\begin{array}{rl} & \left[\mathrm{P}\overline{m+3}\leftarrow f(\mathrm{N}1,...,\mathrm{N}\bar{n},\mathrm{P}1,...,\mathrm{P}\bar{m})\right]\\ \mathrm{L}\overline{r+1} & \mathrm{IF}\;\mathrm{P}\overline{m+1}\ \mathrm{BEGINS\ }a_{1}\text{ }\mathrm{GOTO}\;\mathrm{L}1\\ & \ \ \ \ \ \ \ \ \ \ \ \ \vdots\\ & \mathrm{IF}\;\mathrm{P}\overline{m+1}\ \mathrm{BEGINS\ }a_{r}\text{ }\mathrm{GOTO}\;\mathrm{L}\bar{r}\\ & \mathrm{GOTO}\;\mathrm{L}\overline{r+2}\\ \mathrm{L}1 & \mathrm{P}\overline{m+1}\leftarrow\text{ }^{\curvearrowright}\mathrm{P}\overline{m+1}\\ & \left[\mathrm{P}\overline{m+3}\leftarrow\mathcal{G}_{a_{1}}(\mathrm{N}1,...,\mathrm{N}\bar{n},\mathrm{P}1,...,\mathrm{P}\bar{m},\mathrm{P}\overline{m+2},\mathrm{P}\overline{m+3})\right]\\ & \mathrm{P}\overline{m+2}\leftarrow\mathrm{P}\overline{m+2}.a_{1}\\ & \mathrm{GOTO}\;\mathrm{L}\overline{r+1}\\ & \ \ \ \ \ \ \ \ \ \ \ \ \vdots\\ \mathrm{L}\bar{r} & \mathrm{P}\overline{m+1}\leftarrow\text{ }^{\curvearrowright}\mathrm{P}\overline{m+1}\\ & \left[\mathrm{P}\overline{m+3}\leftarrow\mathcal{G}_{a_{r}}(\mathrm{N}1,...,\mathrm{N}\bar{n},\mathrm{P}1,...,\mathrm{P}\bar{m},\mathrm{P}\overline{m+2},\mathrm{P}\overline{m+3})\right]\\ & \mathrm{P}\overline{m+2}\leftarrow\mathrm{P}\overline{m+2}.a_{r}\\ & \mathrm{GOTO}\;\mathrm{L}\overline{r+1}\\ \mathrm{L}\overline{r+2} & \mathrm{P}1\leftarrow\mathrm{P}\overline{m+3} \end{array}\] Es facil chequear que este programa computa \(h.\)

El resto de los casos son dejados al lector.  

4.4.1.1 Se lleno de macros

Cabe destacar que el corolario anterior nos dice que hay macros \[\begin{aligned} & \left[\mathrm{V}\overline{n+1}\leftarrow f(\mathrm{V}1,...,\mathrm{V}\bar{n},\mathrm{W}1,...,\mathrm{W}\bar{m})\right]\\ & \left[\mathrm{W}\overline{m+1}\leftarrow g(\mathrm{V}1,...,\mathrm{V}\bar{n},\mathrm{W}1,...,\mathrm{W}\bar{m})\right]\\ & \left[\mathrm{IF}\;P(\mathrm{V}1,...,\mathrm{V}\bar{n},\mathrm{W}1,...,\mathrm{W}\bar{m})\;\mathrm{GOTO}\;\mathrm{A}1\right] \end{aligned}\] para todas las funciones \(\Sigma\)-mixtas y predicados \(\Sigma\)-mixtos que hemos trabajado hasta el momento en la materia ya que todas eran \(\Sigma\)-p.r.. Esto transforma al lenguaje \(\mathcal{S}^{\Sigma}\) en un potente y relativamente comodo lenguaje de programacion ya que ahora tenemos macros para todas las funciones y predicados cotidianos en la matematica. Por ejemplo a continuacion usaremos la existencia de los macros \([\mathrm{IF\ V}1\) es par\(\ \mathrm{GOTO\ A}1]\) y \([\mathrm{V}2\leftarrow\lfloor\mathrm{V}1/2\rfloor]\) para probar el siguiente resultado cuya prueba esta inspirada en su analoga del paradigma de computabilidad efectiva.

Proof. Podemos suponer que ni \(S_{1}\) ni \(S_{2}\) son vacios ya que de lo contrario los resultados son triviales. Ademas supondremos que \(n=2\) y \(m=1\).

La idea de la prueba es la misma que la que usamos para probar que la union de conjuntos \(\Sigma\)-efectivamente enumerables es \(\Sigma\)-efectivamente enumerable. Daremos usando macros un programa que enumera a \(S_{1}\cup S_{2}\) y luego aplicaremos la Proposicion 4.10. Por hipotesis hay funciones \(F:\omega\rightarrow\omega\times\omega\times\Sigma^{\ast}\) y \(G:\omega\rightarrow\omega\times\omega\times\Sigma^{\ast}\) tales que \(F_{(1)}\), \(F_{(2)}\), \(F_{(3)}\), \(G_{(1)}\), \(G_{(2)}\) y \(G_{(3)}\) son \(\Sigma\)-computables, \(\operatorname{Im}(F)=S_{1}\) y \(\operatorname{Im}(G)=S_{2}\). O sea que hay macros \[\begin{aligned} & \left[\mathrm{V}2\leftarrow F_{(1)}(\mathrm{V}1)\right]\\ & \left[\mathrm{V}2\leftarrow F_{(2)}(\mathrm{V}1)\right]\\ & \left[\mathrm{W}1\leftarrow F_{(3)}(\mathrm{V}1)\right]\\ & \left[\mathrm{V}2\leftarrow G_{(1)}(\mathrm{V}1)\right]\\ & \left[\mathrm{V}2\leftarrow G_{(2)}(\mathrm{V}1)\right]\\ & \left[\mathrm{W}1\leftarrow G_{(3)}(\mathrm{V}1)\right] \end{aligned}\] Ya que el predicado \(Par=\lambda x[x\) es par\(]\) es \(\Sigma\)-p.r., el Corolario 4.3 nos dice que hay un macro: \[[\mathrm{IF\ }Par(\mathrm{V}1)\ \mathrm{GOTO\ A}1]\] el cual escribiremos de la siguiente manera mas intuitiva \[[\mathrm{IF\ V}1\text{ es par }\mathrm{GOTO\ A}1]\] Ya que la funcion \(D=\lambda x[\lfloor x/2\rfloor]\) es \(\Sigma\)-p.r., el Corolario 4.3 nos dice que hay un macro: \[[\mathrm{V}2\leftarrow D(\mathrm{V}1)]\] el cual escribiremos de la siguiente manera mas intuitiva \[[\mathrm{V}2\leftarrow\lfloor\mathrm{V}1/2\rfloor]\] Sea \(\mathcal{P}\) el siguiente programa: \[\begin{array}{ll} & [\mathrm{IF\ N}1\text{ es par }\mathrm{GOTO\ L}1\\ & \mathrm{N}1\leftarrow\mathrm{N}1\dot{-}1\\ & [\mathrm{N}1111\leftarrow\lfloor\mathrm{N}1/2\rfloor]\\ & \left[\mathrm{N}1\leftarrow G_{(1)}(\mathrm{N}1111)\right]\\ & \left[\mathrm{N}2\leftarrow G_{(2)}(\mathrm{N}1111)\right]\\ & \left[\mathrm{P}1\leftarrow G_{(3)}(\mathrm{N}1111)\right]\\ & \mathrm{GOTO\ L}2\\ \mathrm{L}1 & [\mathrm{N}1111\leftarrow\lfloor\mathrm{N}1/2\rfloor]\\ & \left[\mathrm{N}1\leftarrow F_{(1)}(\mathrm{N}1111)\right]\\ & \left[\mathrm{N}2\leftarrow F_{(2)}(\mathrm{N}1111)\right]\\ & \left[\mathrm{P}1\leftarrow F_{(3)}(\mathrm{N}1111)\right]\\ \mathrm{L}2 & \mathrm{SKIP} \end{array}\] Es facil ver que \(\mathcal{P}\) cumple a y b de (3) de la Proposicion 4.10 por lo cual \(S_{1}\cup S_{2}\) es \(\Sigma\)-enumerable.  

Tal como se vio en este ejemplo, el Corolario 4.3 junto con nuestra gran coleccion de funciones ya probadamente \(\Sigma\)-recursivas, nos permite simular con programas muchos de los procedimientos efectivos realizados anteriormente. Mas capacidad de simulacion obtendremos luego de ver que Godel vence a Neumann ya que la equivalencia de estos dos paradigmas nos asegura la existencia de macros que permitiran dentro de un programa hablar acerca del funcionamiento de otro programa. Esto sera clave a la hora de simular con programas a procedimientos efectivos que en su funcionamiento involucran el funcionamiento de otros procedimientos.

4.4.2 Godel vence a Neumann

Para probar que toda funcion \(\Sigma\)-computable es \(\Sigma\)-recursiva debemos hacer un profundo estudio de la recursividad del lenguaje \(\mathcal{S}^{\Sigma}\). Primero analizaremos la recursividad de la sintaxis de \(\mathcal{S}^{\Sigma}\).

4.4.2.1 Analisis de la recursividad de la sintaxis de \(\mathcal{S}^{\Sigma}\)

Primero probaremos dos lemas que muestran que la sintaxis de \(\mathcal{S}^{\Sigma}\) es \((\Sigma\cup\Sigma_{p})\)-recursiva primitiva. Recordemos que \(Sig:Num^{\ast}\rightarrow Num^{\ast}\) fue definida de la siguiente manera \[\begin{aligned} Sig(\varepsilon) & =1\\ Sig(\alpha0) & =\alpha1\\ Sig(\alpha1) & =\alpha2\\ Sig(\alpha2) & =\alpha3\\ Sig(\alpha3) & =\alpha4\\ Sig(\alpha4) & =\alpha5\\ Sig(\alpha5) & =\alpha6\\ Sig(\alpha6) & =\alpha7\\ Sig(\alpha7) & =\alpha8\\ Sig(\alpha8) & =\alpha9\\ Sig(\alpha9) & =Sig(\alpha)0 \end{aligned}\] Y tambien definimos \(Dec:\omega\rightarrow Num^{\ast}\) de la siguiente manera \[\begin{aligned} Dec(0) & =\varepsilon\\ Dec(n+1) & =Sig(Dec(n)) \end{aligned}\] Recordemos tambien que para hacer mas agil la notacion escribimos \(\bar{n}\) en lugar de \(Dec(n)\).

Es obvio de las definiciones que ambas funciones son \(Num\)-p.r.. Mas aun tenemos

Proof. Es facil ver que \(Sig\) y \(Dec\) son \(Num\)-p.r.. Ya que tambien son \((\Sigma\cup\Sigma_{p})\)-mixtas, el Teorema 4.2 nos dice que ambas son \((\Sigma\cup\Sigma_{p})\)-p.r..  

Recordemos que \(Bas:\mathrm{Ins}^{\Sigma}\rightarrow(\Sigma\cup\Sigma_{p})^{\ast}\), fue definida por \[Bas(I)=\left\{ \begin{array}{ccl} J & & \text{si }I\text{ es de la forma }\mathrm{L}\bar{k}J\text{, con }k\in\mathbf{N}\text{ y }J\in\mathrm{Ins}^{\Sigma}\\ I & & \text{caso contrario} \end{array}\right.\] Definamos \(Lab:\mathrm{Ins}^{\Sigma}\rightarrow(\Sigma\cup\Sigma_{p})^{\ast}\) de la siguiente manera \[Lab(I)=\left\{ \begin{array}{lll} \mathrm{L}\bar{k} & & \text{si }I\text{ es de la forma }\mathrm{L}\bar{k}J\text{, con }k\in\mathbf{N}\text{ y }J\in\mathrm{Ins}^{\Sigma}\\ \varepsilon & & \text{caso contrario} \end{array}\right.\]

Proof. Para simplificar la prueba asumiremos que \(\Sigma=\{@,\blacktriangle\}\). Ya que \(\mathrm{Ins}^{\Sigma}\) es union de los siguientes conjuntos \[\begin{aligned} L_{1} & =\left\{ \mathrm{N}\bar{k}\leftarrow\mathrm{N}\bar{k}+1:k\in\mathbf{N}\right\} \\ L_{2} & =\left\{ \mathrm{N}\bar{k}\leftarrow\mathrm{N}\bar{k}\dot{-}1:k\in\mathbf{N}\right\} \\ L_{3} & =\left\{ \mathrm{N}\bar{k}\leftarrow\mathrm{N}\bar{n}:k,n\in\mathbf{N}\right\} \\ L_{4} & =\left\{ \mathrm{N}\bar{k}\leftarrow0:k\in\mathbf{N}\right\} \\ L_{5} & =\left\{ \mathrm{IF}\;\mathrm{N}\bar{k}\neq0\;\mathrm{GOTO}\;\mathrm{L}\bar{m}:k,m\in\mathbf{N}\right\} \\ L_{6} & =\left\{ \mathrm{P}\bar{k}\leftarrow\mathrm{P}\bar{k}.@:k\in\mathbf{N}\right\} \\ L_{7} & =\left\{ \mathrm{P}\bar{k}\leftarrow\mathrm{P}\bar{k}.\blacktriangle:k\in\mathbf{N}\right\} \\ L_{8} & =\left\{ \mathrm{P}\bar{k}\leftarrow\text{ }^{\curvearrowright}\mathrm{P}\bar{k}:k\in\mathbf{N}\right\} \\ L_{9} & =\left\{ \mathrm{P}\bar{k}\leftarrow\mathrm{P}\bar{n}:k,n\in\mathbf{N}\right\} \\ L_{10} & =\left\{ \mathrm{P}\bar{k}\leftarrow\varepsilon:k\in\mathbf{N}\right\} \\ L_{11} & =\left\{ \mathrm{IF}\;\mathrm{P}\bar{k}\;\mathrm{BEGINS}\;@\;\mathrm{GOTO}\;\mathrm{L}\bar{m}:k,m\in\mathbf{N}\right\} \\ L_{12} & =\left\{ \mathrm{IF}\;\mathrm{P}\bar{k}\;\mathrm{BEGINS}\;\blacktriangle\;\mathrm{GOTO}\;\mathrm{L}\bar{m}:k,m\in\mathbf{N}\right\} \\ L_{13} & =\left\{ \mathrm{GOTO}\;\mathrm{L}\bar{m}:m\in\mathbf{N}\right\} \\ L_{14} & =\left\{ \mathrm{SKIP}\right\} \\ L_{15} & =\left\{ \mathrm{L}\bar{k}\alpha:k\in\mathbf{N\;}\text{y }\alpha\in L_{1}\cup...\cup L_{14}\right\} \end{aligned}\] solo debemos probar que \(L_{1},...,L_{15}\) son \((\Sigma\cup\Sigma_{p})\)-p.r.. Veremos primero por ejemplo que \[L_{11}=\left\{ \mathrm{IFP}\bar{k}\mathrm{BEGINS}@\mathrm{GOTOL}\bar{m}:k,m\in\mathbf{N}\right\}\] es \((\Sigma\cup\Sigma_{p})\)-p.r.. Primero notese que \(\alpha\in L_{11}\) si y solo si existen \(k,m\in\mathbf{N}\) tales que \[\alpha=\mathrm{IFP}\bar{k}\mathrm{BEGINS}@\mathrm{GOTOL}\bar{m}\] Mas formalmente tenemos que \(\alpha\in L_{11}\) si y solo si \[(\exists k\in\mathbf{N})(\exists m\in\mathbf{N})\;\alpha=\mathrm{IFP}\bar{k}\mathrm{BEGINS}@\mathrm{GOTOL}\bar{m}\] Ya que cuando existen tales \(k,m\) tenemos que \(\bar{k}\) y \(\bar{m}\) son subpalabras de \(\alpha\), el lema anterior nos dice que \(\alpha\in L_{11}\) si y solo si \[(\exists k\in\mathbf{N})_{k\leq10^{\left\vert \alpha\right\vert }}(\exists m\in\mathbf{N})_{m\leq10^{\left\vert \alpha\right\vert }}\;\alpha=\mathrm{IFP}\bar{k}\mathrm{BEGINS}@\mathrm{GOTOL}\bar{m}\] Sea \[P=\lambda mk\alpha\left[\alpha=\mathrm{IFP}\bar{k}\mathrm{BEGINS}@\mathrm{GOTOL}\bar{m}\right]\] Ya que \(D_{\lambda k\left[\bar{k}\right]}=\omega\), tenemos que \(D_{P}=\omega^{2}\times(\Sigma\cup\Sigma_{p})^{\ast}\). Notese que \[P=\lambda\alpha\beta\left[\alpha=\beta\right]\circ\left[p_{3}^{2,1},f\right]\] donde \[f=\lambda\alpha_{1}\alpha_{2}\alpha_{3}\alpha_{4}\left[\alpha_{1}\alpha_{2}\alpha_{3}\alpha_{4}\right]\circ\left[C_{\mathrm{IFP}}^{2,1},\lambda k\left[\bar{k}\right]\circ p_{2}^{2,1},C_{\mathrm{BEGINS}@\mathrm{GOTOL}}^{2,1},\lambda k\left[\bar{k}\right]\circ p_{1}^{2,1}\right]\] lo cual nos dice que \(P\) es \((\Sigma\cup\Sigma_{p})\)-p.r..

Notese que \[\chi_{L_{11}}^{(\Sigma\cup\Sigma_{p})^{\ast}}=\lambda\alpha\left[(\exists k\in\mathbf{N})_{k\leq10^{\left\vert \alpha\right\vert }}(\exists m\in\mathbf{N})_{m\leq10^{\left\vert \alpha\right\vert }}\;P(m,k,\alpha)\right]\] Esto nos dice que podemos usar dos veces el Lema 4.21 para ver que \(\chi_{L_{11}}^{(\Sigma\cup\Sigma_{p})^{\ast}}\) es \((\Sigma\cup\Sigma_{p})\)-p.r.. Veamos como. Sea \[Q=\lambda k\alpha\left[(\exists m\in\mathbf{N})_{m\leq10^{\left\vert \alpha\right\vert }}\;P(m,k,\alpha)\right]\] Por el Lema 4.21 tenemos que \[\lambda xk\alpha\left[(\exists m\in\mathbf{N})_{m\leq x}\;P(m,k,\alpha)\right]\] es \((\Sigma\cup\Sigma_{p})\)-p.r. lo cual nos dice que \[Q=\lambda xk\alpha\left[(\exists m\in\mathbf{N})_{m\leq x}\;P(m,k,\alpha)\right]\circ\left[\lambda\alpha\left[10^{\left\vert \alpha\right\vert }\right]\circ p_{2}^{1,1},p_{1}^{1,1},p_{2}^{1,1}\right]\] lo es. Ya que \[\chi_{L_{11}}^{(\Sigma\cup\Sigma_{p})^{\ast}}=\lambda\alpha\left[(\exists k\in\mathbf{N})_{k\leq10^{\left\vert \alpha\right\vert }}\;Q(k,\alpha)\right]\] podemos en forma similar aplicar el Lema 4.21 y obtener finalmente que \(\chi_{L_{11}}^{(\Sigma\cup\Sigma_{p})^{\ast}}\) es \((\Sigma\cup\Sigma_{p})\)-p.r..

En forma similar podemos probar que \(L_{1},...,L_{14}\) son \((\Sigma\cup\Sigma_{p})\)-p.r.. Esto nos dice que \(L_{1}\cup...\cup L_{14}\) es \((\Sigma\cup\Sigma_{p})\)-p.r.. Notese que \(L_{1}\cup...\cup L_{14}\) es el conjunto de las instrucciones basicas de \(\mathcal{S}^{\Sigma}\). Llamemos \(\mathrm{InsBas}^{\Sigma}\) a dicho conjunto. Para ver que \(L_{15}\) es \((\Sigma\cup\Sigma_{p})\)-p.r. notemos que \[\chi_{L_{15}}^{(\Sigma\cup\Sigma_{p})^{\ast}}=\lambda\alpha\left[(\exists k\in\mathbf{N})_{k\leq10^{\left\vert \alpha\right\vert }}(\exists\beta\in\mathrm{InsBas}^{\Sigma})_{\left\vert \beta\right\vert \leq\left\vert \alpha\right\vert }\;\alpha=\mathrm{L}\bar{k}\beta\right]\] lo cual nos dice que aplicando dos veces el Lema 4.21 obtenemos que \(\chi_{L_{15}}^{(\Sigma\cup\Sigma_{p})^{\ast}}\) es \((\Sigma\cup\Sigma_{p})\)-p.r.. Ya que \(\mathrm{Ins}^{\Sigma}=\mathrm{InsBas}^{\Sigma}\cup L_{15}\) tenemos que \(\mathrm{Ins}^{\Sigma}\) es \((\Sigma\cup\Sigma_{p})\)-p.r..  

Proof. Sea \(\leq\) un orden total sobre \(\Sigma\cup\Sigma_{p}\). Sea \(L=\{\mathrm{L}\bar{k}:k\in\mathbf{N}\}\cup\{\varepsilon\}\). Dejamos al lector probar que \(L\) es un conjunto \((\Sigma\cup\Sigma_{p})\)-p.r.. Sea \[P=\lambda I\alpha\left[\alpha\in\mathrm{Ins}^{\Sigma}\wedge I\in\mathrm{Ins}^{\Sigma}\wedge[\alpha]_{1}\neq\mathrm{L}\wedge(\exists\beta\in L)\ I=\beta\alpha\right]\] Note que \(D_{P}=(\Sigma\cup\Sigma_{p})^{\ast2}\). Dejamos al lector probar que \(P\) es \((\Sigma\cup\Sigma_{p})\)-p.r.. Notese ademas que cuando \(I\in\mathrm{Ins}^{\Sigma}\) tenemos que \(P(I,\alpha)=1\) sii \(\alpha=Bas(I)\). Dejamos al lector probar que \(Bas=M^{\leq}\left(P\right)\) por lo que para ver que \(Bas\) es \((\Sigma\cup\Sigma_{p})\)-p.r., solo nos falta ver que la funcion \(Bas\) es acotada por alguna funcion \((\Sigma\cup\Sigma_{p})\)-p.r. y \((\Sigma\cup\Sigma_{p})\)-total. Pero esto es trivial ya que \(\left\vert Bas(I)\right\vert \leq\left\vert I\right\vert =\lambda\alpha[\left\vert \alpha\right\vert ](I)\), para cada \(I\in\mathrm{Ins}^{\Sigma}\).

Finalmente note que \[Lab=M^{\leq}\left(\lambda I\alpha\left[\alpha Bas(I)=I\right]\right)\] lo cual nos dice que \(Lab\) es \((\Sigma\cup\Sigma_{p})\)-p.r..  

Recordemos que dado un programa \(\mathcal{P}\) habiamos definido \(I_{i}^{\mathcal{P}}=\varepsilon\), para \(i=0\) o \(i>n(\mathcal{P}).\) O sea que la funcion \((\Sigma\cup\Sigma_{p})\)-mixta \(\lambda i\mathcal{P}\left[I_{i}^{\mathcal{P}}\right]\) tiene dominio igual a \(\omega\times\mathrm{Pro}^{\Sigma}\). Notese que usamos notacion lambda respecto del alfabeto \(\Sigma\cup\Sigma_{p}\). Ademas notese que usamos la variable \(\mathcal{P}\) en la notacion lambda por un tema de comodidad psicologica dado que la expresion \(I_{i}^{\alpha}\) esta definida solo cuando \(\alpha\) es un programa pero podriamos haber escrito \(\lambda i\alpha\left[I_{i}^{\alpha}\right]\) y sigue siendo la misma funcion.

Proof. Ya que \(\mathrm{Pro}^{\Sigma}=D_{\lambda\mathcal{P}\left[n(\mathcal{P})\right]}\) tenemos que (b) implica (a). Para probar (b) Sea \(\leq\) un orden total sobre \(\Sigma\cup\Sigma_{p}\). Sea \(P\) el siguiente predicado

\(\lambda x\left[Lt(x)>0\wedge(\forall t\in\mathbf{N})_{t\leq Lt(x)}\;\ast^{\leq}((x)_{t})\in\mathrm{Ins}^{\Sigma}\wedge\right.\)

\(\ \ \ \ \ \ \ \ \ \ \ \ (\forall t\in\mathbf{N})_{t\leq Lt(x)}(\forall m\in\mathbf{N})\;\lnot(\mathrm{L}\bar{m}\ \)t-final \(\ast^{\leq}((x)_{t}))\vee\)

\(\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left.(\exists j\in\mathbf{N})_{j\leq Lt(x)}(\exists\alpha\in(\Sigma\cup\Sigma_{p})-Num)\;\mathrm{L}\bar{m}\alpha\ \text{t-inicial}\ast^{\leq}((x)_{j})\right]\)

Notese que \(D_{P}=\mathbf{N}\) y que \(P(x)=1\) sii \(Lt(x)>0\), \(\ast^{\leq}((x)_{t})\in\mathrm{Ins}^{\Sigma}\), para cada \(t=1,...,Lt(x)\) y ademas \(\subset_{t=1}^{t=Lt(x)}\ast^{\leq}((x)_{t})\in\mathrm{Pro}^{\Sigma}\). Para ver que \(P\) es \((\Sigma\cup\Sigma_{p})\)-p.r. solo nos falta acotar el cuantificador \((\forall m\in\mathbf{N})\) de la expresion lambda que define a \(P\). Ya que nos interesan los valores de \(m\) para los cuales \(\bar{m}\) es posiblemente una subpalabra de alguna de las palabras \(\ast^{\leq}((x)_{j})\), el Lema 4.43 nos dice que una cota posible es \(10^{\max\{\left\vert \ast^{\leq}((x)_{j})\right\vert :1\leq j\leq Lt(x)\}}-1\). Dejamos al lector los detalles de la prueba de que \(P\) es \((\Sigma\cup\Sigma_{p})\)-p.r.. Sea \[Q=\lambda x\alpha\left[P(x)\wedge\alpha=\subset_{t=1}^{t=Lt(x)}\ast^{\leq}((x)_{t})\right]\text{.}\] Note que \(D_{Q}=\mathbf{N}\times(\Sigma\cup\Sigma_{p})^{\ast}\). Claramente \(Q\) es \((\Sigma\cup\Sigma_{p})\)-p.r.. Ademas note que \(D_{M(Q)}=\mathrm{Pro}^{\Sigma}\). Notese que para \(\mathcal{P}\in\mathrm{Pro}^{\Sigma}\), tenemos que \(M(Q)(\mathcal{P})\) es aquel numero tal que pensado como infinitupla (via mirar su secuencia de exponentes) codifica la secuencia de instrucciones que forman a \(\mathcal{P}\). Es decir \[M(Q)(\mathcal{P})=\left\langle \#^{\leq}(I_{1}^{\mathcal{P}}),\#^{\leq}(I_{2}^{\mathcal{P}}),...,\#^{\leq}(I_{n(\mathcal{P})}^{\mathcal{P}}),0,0,...\right\rangle\] Por (b) del Lema 4.24, \(M(Q)\) es \((\Sigma\cup\Sigma_{p})\)-p.r. ya que para cada \(\mathcal{P}\in\mathrm{Pro}^{\Sigma}\) tenemos que \[\begin{aligned} M(Q)(\mathcal{P}) & =\left\langle \#^{\leq}(I_{1}^{\mathcal{P}}),\#^{\leq}(I_{2}^{\mathcal{P}}),...,\#^{\leq}(I_{n(\mathcal{P})}^{\mathcal{P}}),0,0,...\right\rangle \\ & =\underset{i=1}{\overset{n(\mathcal{P})}{\Pi}}pr(i)^{\#^{\leq}(I_{1}^{\mathcal{P}})}\\ & \leq\underset{i=1}{\overset{\left\vert \mathcal{P}\right\vert }{\Pi}}pr(i)^{\#^{\leq}(\mathcal{P})} \end{aligned}\] Ademas tenemos que \[\begin{aligned} \lambda\mathcal{P}\left[n(\mathcal{P})\right] & =\lambda x\left[Lt(x)\right]\circ M(Q)\\ \lambda i\mathcal{P}\left[I_{i}^{\mathcal{P}}\right] & =\ast^{\leq}\circ g\circ\left[p_{1}^{1,1},M(Q)\circ p_{2}^{1,1}\right] \end{aligned}\] donde \(g=C_{0}^{1,1}|_{\{0\}\times\omega}\cup\lambda ix\left[(x)_{i}\right]\), lo cual dice que \(\lambda\mathcal{P}\left[n(\mathcal{P})\right]\) y \(\lambda i\mathcal{P}\left[I_{i}^{\mathcal{P}}\right]\) son funciones \((\Sigma\cup\Sigma_{p})\)-p.r..  

4.4.2.2 Analisis de la recursividad de la semantica de \(\mathcal{S}^{\Sigma}\)

Para estudiar la recursividad de la semantica de \(\mathcal{S}^{\Sigma}\) deberemos definir varias funciones que tienen que ver con el funcionamiento de un programa y estudiar su recursividad.

4.4.2.2.1 Las funciones \(i^{n,m}\), \(E_{\#}^{n,m}\) y \(E_{\ast}^{n,m}\)

Sean \(n,m\geq0\) fijos. Definamos entonces las funciones \[\begin{aligned} i^{n,m} & :\omega\times\omega^{n}\times\Sigma^{\ast m}\times\mathrm{Pro}^{\Sigma}\rightarrow\omega\\ E_{\#}^{n,m} & :\omega\times\omega^{n}\times\Sigma^{\ast m}\times\mathrm{Pro}^{\Sigma}\rightarrow\omega^{[\mathbf{N}]}\\ E_{\ast}^{n,m} & :\omega\times\omega^{n}\times\Sigma^{\ast m}\times\mathrm{Pro}^{\Sigma}\rightarrow\Sigma^{\ast[\mathbf{N}]} \end{aligned}\] de la siguiente manera \[\begin{aligned} (i^{n,m}(0,\vec{x},\vec{\alpha},\mathcal{P}),E_{\#}^{n,m}(0,\vec{x},\vec{\alpha},\mathcal{P}),E_{\ast}^{n,m}(0,\vec{x},\vec{\alpha},\mathcal{P})) & =(1,(x_{1},...,x_{n},0,...),(\alpha_{1},...,\alpha_{m},\varepsilon,...))\\ (i^{n,m}(t+1,\vec{x},\vec{\alpha},\mathcal{P}),E_{\#}^{n,m}(t+1,\vec{x},\vec{\alpha},\mathcal{P}),E_{\ast}^{n,m}(t+1,\vec{x},\vec{\alpha},\mathcal{P})) & =S_{\mathcal{P}}(i^{n,m}(t,\vec{x},\vec{\alpha},\mathcal{P}),E_{\#}^{n,m}(t,\vec{x},\vec{\alpha},\mathcal{P}),E_{\ast}^{n,m}(t,\vec{x},\vec{\alpha},\mathcal{P})) \end{aligned}\] Notese que \[(i^{n,m}(t,\vec{x},\vec{\alpha},\mathcal{P}),E_{\#}^{n,m}(t,\vec{x},\vec{\alpha},\mathcal{P}),E_{\ast}^{n,m}(t,\vec{x},\vec{\alpha},\mathcal{P}))\] es la descripcion instantanea que se obtiene luego de correr \(\mathcal{P}\) una cantidad \(t\) de pasos partiendo del estado \[((x_{1},...,x_{n},0,...),(\alpha_{1},...,\alpha_{m},\varepsilon,...))\] Es importante notar que si bien \(i^{n,m}\) es una funcion \((\Sigma\cup\Sigma_{p})\)-mixta, ni \(E_{\#}^{n,m}\) ni \(E_{\ast}^{n,m}\) lo son.

Definamos para cada \(j\in\mathbf{N}\), funciones \[\begin{aligned} E_{\#j}^{n,m} & :\omega\times\omega^{n}\times\Sigma^{\ast m}\times\mathrm{Pro}^{\Sigma}\rightarrow\omega\\ E_{\ast j}^{n,m} & :\omega\times\omega^{n}\times\Sigma^{\ast m}\times\mathrm{Pro}^{\Sigma}\rightarrow\Sigma^{\ast} \end{aligned}\] de la siguiente manera \[\begin{aligned} E_{\#j}^{n,m}(t,\vec{x},\vec{\alpha},\mathcal{P}) & =j\text{-esima coordenada de }E_{\#}^{n,m}(t,\vec{x},\vec{\alpha},\mathcal{P})\\ E_{\ast j}^{n,m}(t,\vec{x},\vec{\alpha},\mathcal{P}) & =j\text{-esima coordenada de }E_{\ast}^{n,m}(t,\vec{x},\vec{\alpha},\mathcal{P}) \end{aligned}\] Notese que \[\begin{aligned} E_{\#}^{n,m}(t,\vec{x},\vec{\alpha},\mathcal{P}) & =(E_{\#1}^{n,m}(t,\vec{x},\vec{\alpha},\mathcal{P}),E_{\#2}^{n,m}(t,\vec{x},\vec{\alpha},\mathcal{P}),...)\\ E_{\ast}^{n,m}(t,\vec{x},\vec{\alpha},\mathcal{P}) & =(E_{\ast1}^{n,m}(t,\vec{x},\vec{\alpha},\mathcal{P}),E_{\ast2}^{n,m}(t,\vec{x},\vec{\alpha},\mathcal{P}),...) \end{aligned}\] Nuestro proximo objetivo es mostrar que las funciones \(i^{n,m}\), \(E_{\#j}^{n,m}\), \(E_{\ast j}^{n,m}\) son \((\Sigma\cup\Sigma_{p})\)-p.r.

Para esto primero debemos probar un lema el cual muestre que una ves codificadas las descripciones instantaneas en forma numerica, las funciones que dan la descripcion instantanea sucesora son \((\Sigma\cup\Sigma_{p})\)-p.r.. Dado un orden total \(\leq\) sobre \(\Sigma\cup\Sigma_{p}\), codificaremos las descripciones instantaneas haciendo uso de las biyecciones \[\begin{array}{rcl} \omega^{\left[\mathbf{N}\right]} & \rightarrow & \mathbf{N}\\ (s_{1},s_{2},...) & \rightarrow & \left\langle s_{1},s_{2},...\right\rangle \end{array}\;\;\;\;\;\;\;\;\;\;\;\;\begin{array}{rcl} \Sigma^{\ast\left[\mathbf{N}\right]} & \rightarrow & \mathbf{N}\\ (\sigma_{1},\sigma_{2},...) & \rightarrow & \left\langle \#^{\leq}(\sigma_{1}),\#^{\leq}(\sigma_{2}),...\right\rangle \end{array}\] Es decir que a la descripcion instantanea \[(i,(s_{1},s_{2},...),(\sigma_{1},\sigma_{2},...))\] la codificaremos con la terna \[(i,\left\langle s_{1},s_{2},...\right\rangle ,\left\langle \#^{\leq}(\sigma_{1}),\#^{\leq}(\sigma_{2}),...\right\rangle )\in\omega\times\mathbf{N}\times\mathbf{N}\] Es decir que una terna \((i,x,y)\in\omega\times\mathbf{N}\times\mathbf{N}\) codificara a la descripcion instantanea \[(i,((x)_{1},(x)_{2},...),(\ast^{\leq}((y)_{1}),\ast^{\leq}((y)_{2}),...))\] Definamos \[\begin{aligned} s & :\omega\times\mathbf{N}\times\mathbf{N}\times\mathrm{Pro}^{\Sigma}\rightarrow\omega\\ S_{\#} & :\omega\times\mathbf{N}\times\mathbf{N}\times\mathrm{Pro}^{\Sigma}\rightarrow\omega\\ S_{\ast} & :\omega\times\mathbf{N}\times\mathbf{N}\times\mathrm{Pro}^{\Sigma}\rightarrow\omega \end{aligned}\] de la siguiente manera \[\begin{array}[t]{ll} s(i,x,y,\mathcal{P})= & \text{primera coordenada de la codificacion de la descripcion instantanea}\\ & \text{sucesora de }(i,((x)_{1},(x)_{2},...),(\ast^{\leq}((y)_{1}),\ast^{\leq}((y)_{2}),...))\text{ en }\mathcal{P} \end{array}\] \[\begin{array}[t]{ll} S_{\#}(i,x,y,\mathcal{P})= & \text{segunda coordenada de la codificacion de la descripcion instantanea}\\ & \text{sucesora de }(i,((x)_{1},(x)_{2},...),(\ast^{\leq}((y)_{1}),\ast^{\leq}((y)_{2}),...))\text{ en }\mathcal{P} \end{array}\] \[\begin{array}[t]{ll} S_{\ast}(i,x,y,\mathcal{P})= & \text{tercera coordenada de la codificacion de la descripcion instantanea}\\ & \text{sucesora de }(i,((x)_{1},(x)_{2},...),(\ast^{\leq}((y)_{1}),\ast^{\leq}((y)_{2}),...))\text{ en }\mathcal{P} \end{array}\] Notese que la definicion de estas funciones depende del orden total \(\leq\) sobre \(\Sigma\cup\Sigma_{p}\).

@@finpagina@@

Proof. Necesitaremos algunas funciones \((\Sigma\cup\Sigma_{p})\)-p.r.. Dada una instruccion \(I\) en la cual al menos ocurre una variable, usaremos \(\#Var1(I)\) para denotar el numero de la primer variable que ocurre en \(I\). Por ejemplo \[\#Var1\left(\mathrm{L}\bar{n}\;\mathrm{IF\;N}\bar{k}\neq0\;\mathrm{GOTO\;L}\bar{m}\right)=k\] Notese que \(\lambda I[\#Var1(I)]\) tiene dominio igual a \(\mathrm{Ins}^{\Sigma}-L\), donde \(L\) es la union de los siguientes conjuntos \[\begin{gathered} \{\mathrm{GOTO\ L}\bar{m}:m\in\mathbf{N\}\cup}\{\mathrm{L}\bar{k}\ \mathrm{GOTO\ L}\bar{m}:k,m\in\mathbf{N\}}\\ \left\{ \mathrm{SKIP}\right\} \mathbf{\cup}\{\mathrm{L}\bar{k}\ \mathrm{SKIP}:k\in\mathbf{N\}} \end{gathered}\] Dada una instruccion \(I\) en la cual ocurren dos variables, usaremos \(\#Var2(I)\) para denotar el numero de la segunda variable que ocurre en \(I\). Por ejemplo \[\#Var2\left(\mathrm{N}\bar{k}\leftarrow\mathrm{N}\bar{m}\right)=m\] Notese que el dominio de \(\lambda I[\#Var2(I)]\) es igual a la union de los siguientes conjuntos \[\begin{aligned} \{\mathrm{N}\bar{k} & \leftarrow\mathrm{N}\bar{m}:k,m\in\mathbf{N\}\cup}\{\mathrm{L}\bar{j}\ \mathrm{N}\bar{k}\leftarrow\mathrm{N}\bar{m}:j,k,m\in\mathbf{N\}}\\ \{\mathrm{P}\bar{k} & \leftarrow\mathrm{P}\bar{m}:k,m\in\mathbf{N\}\cup}\{\mathrm{L}\bar{j}\ \mathrm{P}\bar{k}\leftarrow\mathrm{P}\bar{m}:j,k,m\in\mathbf{N\}} \end{aligned}\] Ademas notese que para una instruccion \(I\) tenemos que \[\begin{aligned} \#Var1(I) & =\min_{k}(\mathrm{N}\bar{k}\mathrm{\leftarrow}\text{ }\mathrm{ocu}\text{ }I\vee\mathrm{N}\bar{k}\mathrm{\neq}\text{ }\mathrm{ocu}\text{ }I\vee\mathrm{P}\bar{k}\mathrm{\leftarrow}\text{ }\mathrm{ocu}\text{ }I\vee\mathrm{P}\bar{k}\mathrm{B}\;\mathrm{ocu}\text{ }I)\\ \#Var2(I) & =\min_{k}(\mathrm{N}\bar{k}\ \text{t-final }I\vee\mathrm{N}\bar{k}\mathrm{+}\text{ }\mathrm{ocu}\text{ }I\vee\mathrm{N}\bar{k}\mathrm{\dot{-}}\text{ }\mathrm{ocu}\text{ }I\vee\mathrm{P}\bar{k}\ \text{t-final }I\vee\mathrm{P}\bar{k}.\text{ }\mathrm{ocu}\text{ }I) \end{aligned}\] Esto nos dice que si llamamos \(P\) al predicado \[\lambda k\alpha\left[\alpha\in\mathrm{Ins}^{\Sigma}\wedge(\mathrm{N}\bar{k}\mathrm{\leftarrow}\text{ }\mathrm{ocu}\text{ }\alpha\vee\mathrm{N}\bar{k}\mathrm{\neq}\text{ }\mathrm{ocu}\text{ }\alpha\vee\mathrm{P}\bar{k}\mathrm{\leftarrow}\text{ }\mathrm{ocu}\text{ }\alpha\vee\mathrm{P}\bar{k}\mathrm{B}\;\mathrm{ocu}\text{ }\alpha)\right]\] entonces \(\lambda I[\#Var1(I)]=M(P)\) por lo cual \(\lambda I[\#Var1(I)]\) es \((\Sigma\cup\Sigma_{p})\)-p.r. Similarmente se puede ver que \(\lambda I[\#Var2(I)]\) es \((\Sigma\cup\Sigma_{p})\)-p.r.. Sea \[\begin{array}{rll} F_{\dot{-}}:\mathbf{N}\times\mathbf{N} & \rightarrow & \omega\\ (x,j) & \rightarrow & \left\langle (x)_{1},....,(x)_{j-1},(x)_{j}\dot{-}1,(x)_{j+1},...\right\rangle \end{array}\] Ya que \[F_{\dot{-}}(x,j)=\left\{ \begin{array}{lll} Q(x,pr(j)) & & \text{si }pr(j)\text{ divide }x\\ x & & \text{caso contrario} \end{array}\right.\] tenemos que \(F_{\dot{-}}\) es \((\Sigma\cup\Sigma_{p})\)-p.r.. Sea \[\begin{array}{rll} F_{+}:\mathbf{N}\times\mathbf{N} & \rightarrow & \omega\\ (x,j) & \rightarrow & \left\langle (x)_{1},....,(x)_{j-1},(x)_{j}+1,(x)_{j+1},...\right\rangle \end{array}\] Ya que \(F_{+}(x,j)=x.pr(j)\) tenemos que \(F_{+}\) es \((\Sigma\cup\Sigma_{p})\)-p.r.. Sea \[\begin{array}{rll} F_{\leftarrow}:\mathbf{N}\times\mathbf{N}\times\mathbf{N} & \rightarrow & \omega\\ (x,j,k) & \rightarrow & \left\langle (x)_{1},....,(x)_{j-1},(x)_{k},(x)_{j+1},...\right\rangle \end{array}\] Ya que \(F_{\leftarrow}(x,j,k)=Q(x,pr(j)^{(x)_{j}}).pr(j)^{(x)_{k}}\) tenemos que \(F_{\leftarrow}\) es \((\Sigma\cup\Sigma_{p})\)-p.r.. Sea \[\begin{array}{rll} F_{0}:\mathbf{N}\times\mathbf{N} & \rightarrow & \omega\\ (x,j) & \rightarrow & \left\langle (x)_{1},....,(x)_{j-1},0,(x)_{j+1},...\right\rangle \end{array}\] Es facil ver que \(F_{0}\) es \((\Sigma\cup\Sigma_{p})\)-p.r.. Para cada \(a\in\Sigma\), sea \[\begin{array}{rll} F_{a}:\mathbf{N}\times\mathbf{N} & \rightarrow & \omega\\ (x,j) & \rightarrow & \left\langle (x)_{1},....,(x)_{j-1},\#^{\leq}(\ast^{\leq}((x)_{j})a),(x)_{j+1},...\right\rangle \end{array}\] Es facil ver que \(F_{a}\) es \((\Sigma\cup\Sigma_{p})\)-p.r.. En forma similar puede ser probado que \[\begin{array}{rll} F_{\curvearrowright}:\mathbf{N}\times\mathbf{N} & \rightarrow & \omega\\ (x,j) & \rightarrow & \left\langle (x)_{1},....,(x)_{j-1},\#^{\leq}(^{\curvearrowright}(\ast^{\leq}((x)_{j}))),(x)_{j+1},...\right\rangle \end{array}\] es \((\Sigma\cup\Sigma_{p})\)-p.r.

Dado \((i,x,y,\mathcal{P})\in\omega\times\mathbf{N}\times\mathbf{N}\times\mathrm{Pro}^{\Sigma}\), tenemos varios casos en los cuales los valores \(s(i,x,y,\mathcal{P}),S_{\#}(i,x,y,\mathcal{P})\) y \(S_{\ast}(i,x,y,\mathcal{P})\) pueden ser obtenidos usando las funciones antes definidas:

1. adhocprefix(1)adhocsufix CASO \(i=0\vee i>n(\mathcal{P})\). Entonces \[\begin{aligned} s(i,x,y,\mathcal{P}) & =i\\ S_{\#}(i,x,y,\mathcal{P}) & =x\\ S_{\ast}(i,x,y,\mathcal{P}) & =y \end{aligned}\]

2. adhocprefix(2)adhocsufix CASO \((\exists j\in\omega)\;Bas(I_{i}^{\mathcal{P}})=\mathrm{N}\bar{j}\leftarrow\mathrm{N}\bar{j}+1\). Entonces \[\begin{aligned} s(i,x,y,\mathcal{P}) & =i+1\\ S_{\#}(i,x,y,\mathcal{P}) & =F_{+}(x,\#Var1(I_{i}^{\mathcal{P}}))\\ S_{\ast}(i,x,y,\mathcal{P}) & =y \end{aligned}\]

3. adhocprefix(3)adhocsufix CASO \((\exists j\in\omega)\;Bas(I_{i}^{\mathcal{P}})=\mathrm{N}\bar{j}\leftarrow\mathrm{N}\bar{j}\dot{-}1\). Entonces \[\begin{aligned} s(i,x,y,\mathcal{P}) & =i+1\\ S_{\#}(i,x,y,\mathcal{P}) & =F_{\dot{-}}(x,\#Var1(I_{i}^{\mathcal{P}}))\\ S_{\ast}(i,x,y,\mathcal{P}) & =y \end{aligned}\]

4. adhocprefix(4)adhocsufix CASO \((\exists j,k\in\omega)\;Bas(I_{i}^{\mathcal{P}})=\mathrm{N}\bar{j}\leftarrow\mathrm{N}\bar{k}\). Entonces \[\begin{aligned} s(i,x,y,\mathcal{P}) & =i+1\\ S_{\#}(i,x,y,\mathcal{P}) & =F_{\leftarrow}(x,\#Var1(I_{i}^{\mathcal{P}}),\#Var2(I_{i}^{\mathcal{P}}))\\ S_{\ast}(i,x,y,\mathcal{P}) & =y \end{aligned}\]

5. adhocprefix(5)adhocsufix CASO \((\exists j,k\in\omega)\;Bas(I_{i}^{\mathcal{P}})=\mathrm{N}\bar{j}\leftarrow0\). Entonces \[\begin{aligned} s(i,x,y,\mathcal{P}) & =i+1\\ S_{\#}(i,x,y,\mathcal{P}) & =F_{0}(x,\#Var1(I_{i}^{\mathcal{P}}))\\ S_{\ast}(i,x,y,\mathcal{P}) & =y \end{aligned}\]

6. adhocprefix(6)adhocsufix CASO \((\exists j,m\in\omega)\;\left(Bas(I_{i}^{\mathcal{P}})=\mathrm{IF}\;\mathrm{N}\bar{j}\neq0\;\mathrm{GOTO}\;\mathrm{L}\bar{m}\wedge(x)_{j}=0\right)\). Entonces \[\begin{aligned} s(i,x,y,\mathcal{P}) & =i+1\\ S_{\#}(i,x,y,\mathcal{P}) & =x\\ S_{\ast}(i,x,y,\mathcal{P}) & =y \end{aligned}\]

7. adhocprefix(7)adhocsufix CASO \((\exists j,m\in\omega)\;\left(Bas(I_{i}^{\mathcal{P}})=\mathrm{IF}\;\mathrm{N}\bar{j}\neq0\;\mathrm{GOTO}\;\mathrm{L}\bar{m}\wedge(x)_{j}\neq0\right)\). Entonces \[\begin{aligned} s(i,x,y,\mathcal{P}) & =\min_{l}\left(Lab(I_{l}^{\mathcal{P}})\neq\varepsilon\wedge Lab(I_{l}^{\mathcal{P}})\text{ }\mathrm{t}\text{\textrm{-final} }I_{i}^{\mathcal{P}}\right)\\ S_{\#}(i,x,y,\mathcal{P}) & =x\\ S_{\ast}(i,x,y,\mathcal{P}) & =y \end{aligned}\]

8. adhocprefix(8)adhocsufix CASO \((\exists j\in\omega)\;Bas(I_{i}^{\mathcal{P}})=\mathrm{P}\bar{j}\leftarrow\mathrm{P}\bar{j}.a\). Entonces \[\begin{aligned} s(i,x,y,\mathcal{P}) & =i+1\\ S_{\#}(i,x,y,\mathcal{P}) & =x\\ S_{\ast}(i,x,y,\mathcal{P}) & =F_{a}(y,\#Var1(I_{i}^{\mathcal{P}})) \end{aligned}\]

9. adhocprefix(9)adhocsufix CASO \((\exists j\in\omega)\;Bas(I_{i}^{\mathcal{P}})=\mathrm{P}\bar{j}\leftarrow\) \(^{\curvearrowright}\mathrm{P}\bar{j}\). Entonces \[\begin{aligned} s(i,x,y,\mathcal{P}) & =i+1\\ S_{\#}(i,x,y,\mathcal{P}) & =x\\ S_{\ast}(i,x,y,\mathcal{P}) & =F_{\curvearrowright}(y,\#Var1(I_{i}^{\mathcal{P}})) \end{aligned}\]

10. adhocprefix(10)adhocsufix CASO \((\exists j,k\in\omega)\;Bas(I_{i}^{\mathcal{P}})=\mathrm{P}\bar{j}\leftarrow\mathrm{P}\bar{k}\). Entonces \[\begin{aligned} s(i,x,y,\mathcal{P}) & =i+1\\ S_{\#}(i,x,y,\mathcal{P}) & =x\\ S_{\ast}(i,x,y,\mathcal{P}) & =F_{\leftarrow}(y,\#Var1(I_{i}^{\mathcal{P}}),\#Var2(I_{i}^{\mathcal{P}})) \end{aligned}\]

11. adhocprefix(11)adhocsufix CASO \((\exists j\in\omega)\;Bas(I_{i}^{\mathcal{P}})=\mathrm{P}\bar{j}\leftarrow\varepsilon\). Entonces \[\begin{aligned} s(i,x,y,\mathcal{P}) & =i+1\\ S_{\#}(i,x,y,\mathcal{P}) & =x\\ S_{\ast}(i,x,y,\mathcal{P}) & =F_{0}(y,\#Var1(I_{i}^{\mathcal{P}})) \end{aligned}\]

12. adhocprefix(12)adhocsufix CASO \((\exists j,m\in\omega)(\exists a\in\Sigma)\;\left(Bas(I_{i}^{\mathcal{P}})=\mathrm{IF}\;\mathrm{P}\bar{j}\;\mathrm{BEGINS}\;a\;\mathrm{GOTO}\;\mathrm{L}\bar{m}\wedge[\ast^{\leq}((y)_{j})]_{1}\neq a\right)\). Entonces \[\begin{aligned} s(i,x,y,\mathcal{P}) & =i+1\\ S_{\#}(i,x,y,\mathcal{P}) & =x\\ S_{\ast}(i,x,y,\mathcal{P}) & =y \end{aligned}\]

13. adhocprefix(13)adhocsufix CASO \((\exists j,m\in\omega)(\exists a\in\Sigma)\;\left(Bas(I_{i}^{\mathcal{P}})=\mathrm{IF\;P}\bar{j}\;\mathrm{BEGINS\;}a\;\mathrm{GOTO\;L}\bar{m}\wedge[\ast^{\leq}((y)_{j})]_{1}=a\right)\). Entonces \[\begin{aligned} s(i,x,y,\mathcal{P}) & =\min_{l}\left(Lab(I_{l}^{\mathcal{P}})\neq\varepsilon\wedge Lab(I_{l}^{\mathcal{P}})\text{ }\mathrm{t}\text{\textrm{-final} }I_{i}^{\mathcal{P}}\right)\\ S_{\#}(i,x,y,\mathcal{P}) & =x\\ S_{\ast}(i,x,y,\mathcal{P}) & =y \end{aligned}\]

14. adhocprefix(14)adhocsufix CASO \((\exists j\in\omega)\;Bas(I_{i}^{\mathcal{P}})=\mathrm{GOTO}\) \(\mathrm{L}\bar{j}\). Entonces \[\begin{aligned} s(i,x,y,\mathcal{P}) & =\min_{l}\left(Lab(I_{l}^{\mathcal{P}})\neq\varepsilon\wedge Lab(I_{l}^{\mathcal{P}})\text{ }\mathrm{t}\text{\textrm{-final} }I_{i}^{\mathcal{P}}\right)\\ S_{\#}(i,x,y,\mathcal{P}) & =x\\ S_{\ast}(i,x,y,\mathcal{P}) & =y \end{aligned}\]

15. adhocprefix(15)adhocsufix CASO \(Bas(I_{i}^{\mathcal{P}})=\mathrm{SKIP}\). Entonces \[\begin{aligned} s(i,x,y,\mathcal{P}) & =i+1\\ S_{\#}(i,x,y,\mathcal{P}) & =x\\ S_{\ast}(i,x,y,\mathcal{P}) & =y \end{aligned}\]

O sea que los casos anteriores nos permiten definir conjuntos \(S_{1},...,S_{15}\), los cuales son disjuntos de a pares y cuya union da el conjunto \(\omega\times\mathbf{N}\times\mathbf{N}\times\mathrm{Pro}^{\Sigma}\), de manera que cada una de las funciones \(s,S_{\#}\) y \(S_{\ast}\) pueden escribirse como union disjunta de funciones \((\Sigma\cup\Sigma_{p})\)-p.r. restrinjidas respectivamente a los conjuntos \(S_{1},...,S_{15}\). Ya que los conjuntos \(S_{1},...,S_{15}\) son \((\Sigma\cup\Sigma_{p})\)-p.r. el Lema 4.18 nos dice que \(s,S_{\#}\) y \(S_{\ast}\) lo son.  

Aparte del lema anterior, para probar que las funciones \(i^{n,m}\), \(E_{\#j}^{n,m}\) y \(E_{\ast j}^{n,m}\) son \((\Sigma\cup\Sigma_{p})\)-p.r., nos sera necesario el siguiente resultado. Recordemos que para \(x_{1},...,x_{n}\in\omega\), usabamos \(\left\langle x_{1},...,x_{n}\right\rangle\) para denotar \(\left\langle x_{1},...,x_{n},0,...\right\rangle\). Ademas recordemos que en el Lema 4.27 probamos que para cada \(n\geq1\), la funcion \(\lambda x_{1}...x_{n}\left[\left\langle x_{1},...,x_{n}\right\rangle \right]\) es \(\emptyset\)-p.r.

Proof. Para mayor claridad haremos el caso \(k=2\). Sea \[F=\lambda t\vec{x}\vec{\alpha}\left[\left\langle F_{1}(t,\vec{x},\vec{\alpha}),F_{2}(t,\vec{x},\vec{\alpha})\right\rangle \right]\] Es claro que si \(F\) es \(\Sigma\)-p.r., entonces lo es cada \(F_{i}\). Notese que \[\begin{aligned} F(0,\vec{x},\vec{\alpha}) & =\left\langle f_{1}(\vec{x},\vec{\alpha}),f_{2}(\vec{x},\vec{\alpha})\right\rangle \\ F(t+1,\vec{x},\vec{\alpha}) & =\left\langle g_{1}((F(t,\vec{x},\vec{\alpha}))_{1},(F(t,\vec{x},\vec{\alpha}))_{2},t,\vec{x},\vec{\alpha}),g_{2}((F(t,\vec{x},\vec{\alpha}))_{1},(F(t,\vec{x},\vec{\alpha}))_{2},t,\vec{x},\vec{\alpha})\right\rangle \end{aligned}\] lo cual nos dice que \(F=R(f,g)\) donde \[\begin{aligned} f & =\lambda\vec{x}\vec{\alpha}\left[\left\langle f_{1}(\vec{x},\vec{\alpha}),f_{2}(\vec{x},\vec{\alpha})\right\rangle \right]\\ g & =\lambda At\vec{x}\vec{\alpha}\left[\left\langle g_{1}((A)_{1},(A)_{2},t,\vec{x},\vec{\alpha}),g_{2}((A)_{1},(A)_{2},t,\vec{x},\vec{\alpha})\right\rangle \right] \end{aligned}\]  

Ahora usando los dos lemas anteriores podemos probar el siguiente importante resultado.

Proof. Sea \(\leq\) un orden total sobre \(\Sigma\cup\Sigma_{p}\) y sean \(s\), \(S_{\#}\) y \(S_{\ast}\) las funciones definidas previamente al Lema 4.46. Definamos \[\begin{aligned} K_{\#}^{n,m} & =\lambda t\vec{x}\vec{\alpha}\mathcal{P}\left[\left\langle E_{\#1}^{n,m}(t,\vec{x},\vec{\alpha},\mathcal{P}),E_{\#2}^{n,m}(t,\vec{x},\vec{\alpha},\mathcal{P}),...\right\rangle \right]\\ K_{\ast}^{n,m} & =\lambda t\vec{x}\vec{\alpha}\mathcal{P}\left[\left\langle \#^{\leq}(E_{\ast1}^{n,m}(t,\vec{x},\vec{\alpha},\mathcal{P})),\#^{\leq}(E_{\ast2}^{n,m}(t,\vec{x},\vec{\alpha},\mathcal{P})),...\right\rangle \right] \end{aligned}\] Notese que \[\begin{aligned} i^{n,m}(0,\vec{x},\vec{\alpha},\mathcal{P}) & =1\\ K_{\#}^{n,m}(0,\vec{x},\vec{\alpha},\mathcal{P}) & =\left\langle x_{1},...,x_{n}\right\rangle \\ K_{\ast}^{n,m}(0,\vec{x},\vec{\alpha},\mathcal{P}) & =\left\langle \#^{\leq}(\alpha_{1}),...,\#^{\leq}(\alpha_{m})\right\rangle \\ i^{n,m}(t+1,\vec{x},\vec{\alpha},\mathcal{P}) & =s(i^{n,m}(t,\vec{x},\vec{\alpha},\mathcal{P}),K_{\#}^{n,m}(t,\vec{x},\vec{\alpha},\mathcal{P}),K_{\ast}^{n,m}(t,\vec{x},\vec{\alpha},\mathcal{P}))\\ K_{\#}^{n,m}(t+1,\vec{x},\vec{\alpha},\mathcal{P}) & =S_{\#}(i^{n,m}(t,\vec{x},\vec{\alpha},\mathcal{P}),K_{\#}^{n,m}(t,\vec{x},\vec{\alpha},\mathcal{P}),K_{\ast}^{n,m}(t,\vec{x},\vec{\alpha},\mathcal{P}))\\ K_{\ast}^{n,m}(t+1,\vec{x},\vec{\alpha},\mathcal{P}) & =S_{\ast}(i^{n,m}(t,\vec{x},\vec{\alpha},\mathcal{P}),K_{\#}^{n,m}(t,\vec{x},\vec{\alpha},\mathcal{P}),K_{\ast}^{n,m}(t,\vec{x},\vec{\alpha},\mathcal{P})) \end{aligned}\] Por el Lema 4.47 tenemos que \(i^{n,m}\), \(K_{\#}^{n,m}\) y \(K_{\ast}^{n,m}\) son \((\Sigma\cup\Sigma_{p})\)-p.r.. Ademas notese que \[\begin{aligned} E_{\#j}^{n,m} & =\lambda t\vec{x}\vec{\alpha}\mathcal{P}\left[(K_{\#}^{n,m}(t,\vec{x},\vec{\alpha},\mathcal{P}))_{j}\right]\\ E_{\ast j}^{n,m} & =\lambda t\vec{x}\vec{\alpha}\mathcal{P}\left[\ast^{\leq}((K_{\ast}^{n,m}(t,\vec{x},\vec{\alpha},\mathcal{P}))_{j})\right] \end{aligned}\] por lo cual las funciones \(E_{\#j}^{n,m}\), \(E_{\ast j}^{n,m}\), \(j=1,2,...\), son \((\Sigma\cup\Sigma_{p})\)-p.r.  

4.4.2.2.2 Las funciones \(Halt^{n,m}\) y \(T^{n,m}\)

Dados \(n,m\in\omega\), definamos: \[Halt^{n,m}=\lambda t\vec{x}\vec{\alpha}\mathcal{P}\left[i^{n,m}(t,\vec{x},\vec{\alpha},\mathcal{P})=n(\mathcal{P})+1\right]\] Notese que \(D_{Halt^{n,m}}=\omega\times\omega^{n}\times\Sigma^{\ast m}\times\mathrm{Pro}^{\Sigma}\) (ojo que aqui la notacion lambda es respecto del alfabeto \(\Sigma\cup\Sigma_{p}\)). Ademas notese que usamos la variable \(\mathcal{P}\) en la notacion lambda por un tema de comodidad psicologica dado que \(i^{n,m}\) esta definida solo cuando la ultima coordenada es un programa pero podriamos haber escrito \(\lambda t\vec{x}\vec{\alpha}\alpha\left[i^{n,m}(t,\vec{x},\vec{\alpha},\alpha)=n(\alpha)+1\right]\) y sigue siendo la misma funcion.

Cabe destacar que \(Halt^{n,m}\) tiene una descripcion muy intuitiva, ya que dado \((t,\vec{x},\vec{\alpha},\mathcal{P})\in\omega\times\omega^{n}\times\Sigma^{\ast m}\times\mathrm{Pro}^{\Sigma}\), tenemos que \(Halt^{n,m}(t,\vec{x},\vec{\alpha},\mathcal{P})=1\) si y solo si el programa \(\mathcal{P}\) se detiene luego de \(t\) pasos partiendo desde el estado \(\left\Vert x_{1},...,x_{n},\alpha_{1},...,\alpha_{m}\right\Vert\).

Proof. Notar que \(Halt^{n,m}=\lambda xy[x=y]\circ\left[i^{n,m},\lambda\mathcal{P}[n(\mathcal{P})+1]\circ p_{1+n+m+1}^{1+n,m+1}\right]\).  

Ahora definamos \(T^{n,m}=M(Halt^{n,m})\). Notese que \[D_{T^{n,m}}=\{(\vec{x},\vec{\alpha},\mathcal{P}):\mathcal{P}\text{ se detiene partiendo de }\left\Vert x_{1},...,x_{n},\alpha_{1},...,\alpha_{m}\right\Vert \}\] y para \((\vec{x},\vec{\alpha},\mathcal{P})\in D_{T^{n,m}}\) tenemos que \(T^{n,m}(\vec{x},\vec{\alpha},\mathcal{P})=\) cantidad de pasos necesarios para que \(\mathcal{P}\) se detenga partiendo de \(\left\Vert x_{1},...,x_{n},\alpha_{1},...,\alpha_{m}\right\Vert\). En algun sentido, la funcion \(T^{n,m}\) mide el tiempo que tarda en detenerse \(\mathcal{P}\)

Proof. Es directo del Lema 4.24 ya que \(Halt^{n,m}\) es \((\Sigma\cup\Sigma_{p})\)-p.r.  

4.4.2.2.3 Las funciones \(\Phi_{\#}^{n,m}\) y \(\Phi_{\ast}^{n,m}\)

Para \(n,m\in\omega\) definamos la funcion \(\Phi_{\#}^{n,m}\) de la siguiente manera: \[\begin{aligned} D_{\Phi_{\#}^{n,m}} & =\left\{ (\vec{x},\vec{\alpha},\mathcal{P})\in\omega^{n}\times\Sigma^{\ast m}\times\mathrm{Pro}^{\Sigma}:(\vec{x},\vec{\alpha})\in D_{\Psi_{\mathcal{P}}^{n,m,\#}}\right\} \\ \Phi_{\#}^{n,m}(\vec{x},\vec{\alpha},\mathcal{P}) & =\Psi_{\mathcal{P}}^{n,m,\#}(\vec{x},\vec{\alpha})\text{, para cada }(\vec{x},\vec{\alpha},\mathcal{P})\in D_{\Phi_{\#}^{n,m}} \end{aligned}\] Notese que \[D_{\Phi_{\#}^{n,m}}=\{(\vec{x},\vec{\alpha},\mathcal{P}):\mathcal{P}\text{ se detiene partiendo de }\left\Vert x_{1},...,x_{n},\alpha_{1},...,\alpha_{m}\right\Vert \}\] y para cada \((\vec{x},\vec{\alpha},\mathcal{P})\in D_{\Phi_{\#}^{n,m}}\), se tiene que \(\Phi_{\#}^{n,m}(\vec{x},\vec{\alpha},\mathcal{P})=\) valor que queda en la variable \(\mathrm{N}1\) cuando \(\mathcal{P}\) se detiene partiendo de \(\left\Vert x_{1},...,x_{n},\alpha_{1},...,\alpha_{m}\right\Vert\).

Similarmente, definamos la funcion \(\Phi_{\ast}^{n,m}\) de la siguiente manera: \[\begin{aligned} D_{\Phi_{\ast}^{n,m}} & =\left\{ (\vec{x},\vec{\alpha},\mathcal{P})\in\omega^{n}\times\Sigma^{\ast m}\times\mathrm{Pro}^{\Sigma}:(\vec{x},\vec{\alpha})\in D_{\Psi_{\mathcal{P}}^{n,m,\ast}}\right\} \\ \Phi_{\ast}^{n,m}(\vec{x},\vec{\alpha},\mathcal{P}) & =\Psi_{\mathcal{P}}^{n,m,\ast}(\vec{x},\vec{\alpha})\text{, para cada }(\vec{x},\vec{\alpha},\mathcal{P})\in D_{\Phi_{\ast}^{n,m}} \end{aligned}\] Notese que \[\begin{aligned} \Phi_{\#}^{n,m} & =\lambda\vec{x}\vec{\alpha}\mathcal{P}\left[\Psi_{\mathcal{P}}^{n,m,\#}(\vec{x},\vec{\alpha})\right]\\ \Phi_{\ast}^{n,m} & =\lambda\vec{x}\vec{\alpha}\mathcal{P}\left[\Psi_{\mathcal{P}}^{n,m,\ast}(\vec{x},\vec{\alpha})\right] \end{aligned}\]

Proof. Veremos que \(\Phi_{\#}^{n,m}\) es \((\Sigma\cup\Sigma_{p})\)-recursiva. Notar que \(D_{T^{n,m}}=D_{\Phi_{\#}^{n,m}}\). Notese que para \((\vec{x},\vec{\alpha},\mathcal{P})\in D_{T^{n,m}}=D_{\Phi_{\#}^{n,m}}\) tenemos que \[\Phi_{\#}^{n,m}(\vec{x},\vec{\alpha},\mathcal{P})=E_{\#1}^{n,m}\left(T^{n,m}(\vec{x},\vec{\alpha},\mathcal{P}),\vec{x},\vec{\alpha},\mathcal{P}\right)\] lo cual con un poco mas de trabajo nos permite probar que \[\Phi_{\#}^{n,m}=E_{\#1}^{n,m}\circ\left[T^{n,m},p_{1}^{n,m+1},...,p_{n+m+1}^{n,m+1}\right]\] Ya que la funcion \(E_{\#1}^{n,m}\) es \((\Sigma\cup\Sigma_{p})\)-p.r. y \(T^{n,m}\) es \((\Sigma\cup\Sigma_{p})\)-r., tenemos que \(\Phi_{\#}^{n,m}\) es \((\Sigma\cup\Sigma_{p})\)-r.  

4.4.2.3 Godel vence a Neumann

Ahora nos sera facil probar que el paradigma de Godel es por lo menos tan abarcativo como el imperativo de Von Neumann. Mas concretamente:

Proof. Haremos el caso \(O=\Sigma^{\ast}\). Sea \(\mathcal{P}_{0}\) un programa que compute a \(f\). Primero veremos que \(f\) es \((\Sigma\cup\Sigma_{p})\)-recursiva. Note que \[f=\Phi_{\ast}^{n,m}\circ\left[p_{1}^{n,m},...,p_{n+m}^{n,m},C_{\mathcal{P}_{0}}^{n,m}\right]\] donde cabe destacar que \(p_{1}^{n,m},...,p_{n+m}^{n,m}\) son las proyecciones respecto del alfabeto \(\Sigma\cup\Sigma_{p}\), es decir que tienen dominio \(\omega^{n}\times(\Sigma\cup\Sigma_{p})^{\ast m}\). Ya que \(\Phi_{\ast}^{n,m}\) es \((\Sigma\cup\Sigma_{p})\)-recursiva tenemos que \(f\) lo es. O sea que el Teorema 4.2 nos dice que \(f\) es \(\Sigma\)-recursiva.  

Un corolario interesante que se puede obtener del teorema anterior es que toda funcion \(\Sigma\)-recursiva puede obtenerse combinando las reglas basicas en una forma muy particular.

Proof. Supongamos que \(O=\Sigma^{\ast}\). Sea \(\mathcal{P}_{0}\) un programa el cual compute a \(f\). Sea \(\leq\) un orden total sobre \(\Sigma\). Note que podemos tomar \[\begin{aligned} P & =\lambda t\vec{x}\vec{\alpha}[Halt^{n,m}\left((t)_{1},\vec{x},\vec{\alpha},\mathcal{P}_{0}\right)\wedge(t)_{2}=\#^{\leq}(E_{\ast1}^{n,m}((t)_{1},\vec{x},\vec{\alpha},\mathcal{P}_{0}))]\\ g & =\lambda t\left[\ast^{\leq}((t)_{2})\right] \end{aligned}\] (Justifique por que \(P\) es \(\Sigma\)-p.r..)  

A continuacion veremos ejemplos naturales de funciones \((\Sigma\cup\Sigma_{p})\)-recursivas que no son \((\Sigma\cup\Sigma_{p})\)-recursivas primitivas. Cabe destacar que la prueba se basa en la Proposicion 4.6 (enunciada sin demostracion) la cual nos dice que cualquiera sea el alfabeto finito \(\Sigma\), siempre hay una funcion que es \(\Sigma\)-recursiva y no es \(\Sigma\)-recursiva primitiva

Proof. Fijemos \(n,m\in\omega\). Probaremos que \(\Phi_{\#}^{n,m}\) es \((\Sigma\cup\Sigma_{p})\)-p.r. sii \(\Phi_{\#}^{0,0}\) es \((\Sigma\cup\Sigma_{p})\)-p.r.. Sean \(f_{1},f_{2}:\omega^{n}\times\Sigma^{\ast m}\rightarrow(\Sigma\cup\Sigma_{p})^{\ast}\) dadas por \[\begin{aligned} f_{1}(\vec{x},\vec{\alpha}) & =(\mathrm{N}1\leftarrow\mathrm{N}1+1)^{x_{1}}...(\mathrm{N}\bar{n}\leftarrow\mathrm{N}\bar{n}+1)^{x_{n}}\\ f_{1}(\vec{x},\vec{\alpha}) & =\left(\subset_{i=1}^{i=\left\vert \alpha_{1}\right\vert }\mathrm{P}1\leftarrow\mathrm{P}1.[\alpha_{1}]_{i}\right)...\left(\subset_{i=1}^{i=\left\vert \alpha_{m}\right\vert }\mathrm{P}1\leftarrow\mathrm{P}1.[\alpha_{m}]_{i}\right) \end{aligned}\] Sea \(f:\omega^{n}\times\Sigma^{\ast m}\times\mathrm{Pro}^{\Sigma}\rightarrow(\Sigma\cup\Sigma_{p})^{\ast}\) dada por \[f(\vec{x},\vec{\alpha},\mathcal{P})=f_{1}(\vec{x},\vec{\alpha})f_{1}(\vec{x},\vec{\alpha})\mathcal{P}\] Es facil ver que \(f\) es \((\Sigma\cup\Sigma_{p})\)-p.r.. Notese que \(\Phi_{\#}^{n,m}=\Phi_{\#}^{0,0}\circ f\). Ademas notese que \[\Phi_{\#}^{0,0}=\Phi_{\#}^{n,m}\circ\left[C_{0}^{0,1},...,C_{0}^{0,1},C_{\varepsilon}^{0,1},...,C_{\varepsilon}^{0,1},p_{1}^{0,1}\right]\] Ya que \(f\) y las funciones \(C_{0}^{0,1},C_{\varepsilon}^{0,1},p_{1}^{0,1}\) son \((\Sigma\cup\Sigma_{p})\)-p.r., tenemos que \(\Phi_{\#}^{n,m}\) es \((\Sigma\cup\Sigma_{p})\)-p.r. sii \(\Phi_{\#}^{0,0}\) lo es.

Supongamos ahora que para algunos \(k,l\in\omega\) se tiene que \(\Phi_{\#}^{k,l}\) es \((\Sigma\cup\Sigma_{p})\)-p.r.. Llegaremos a un absurdo. Por lo antes probado tenemos que \(\Phi_{\#}^{n,m}\) es \((\Sigma\cup\Sigma_{p})\)-p.r., cualesquiera sean \(n,m\in\omega\). Notese que de la prueba del teorema anterior sigue que toda funcion \(\Sigma\)-computable con imagen contenida en \(\omega\) es de la forma \(\Phi_{\#}^{n,m}\circ\left[p_{1}^{n,m},...,p_{n+m}^{n,m},C_{\mathcal{P}_{0}}^{n,m}\right]\), para algunos \(n,m\in\omega\) y \(\mathcal{P}_{0}\in\mathrm{Pro}^{\Sigma}\). Pero entonces toda funcion \(\Sigma\)-computable con imagen contenida en \(\omega\) es \((\Sigma\cup\Sigma_{p})\)-p.r., lo cual por el Teorema 4.5 nos dice que toda funcion \(\Sigma\)-computable con imagen contenida en \(\omega\) es \((\Sigma\cup\Sigma_{p})\)-p.r.. Esto contradice la Proposicion 4.6.

Ahora supongamos que hay \(n,m\in\omega\) tales que \(T^{n,m}\) es \((\Sigma\cup\Sigma_{p})\)-p.r.. Llegaremos a un absurdo. Como ya vimos en la prueba de un teorema reciente, se tiene que \[\Phi_{\#}^{n,m}=E_{\#1}^{n,m}\circ\left[T^{n,m},p_{1}^{n,m+1},...,p_{n+m+1}^{n,m+1}\right]\] Pero entonces ya que \(E_{\#1}^{n,m}\) es \((\Sigma\cup\Sigma_{p})\)-p.r., tenemos que \(\Phi_{\#}^{n,m}\) es \((\Sigma\cup\Sigma_{p})\)-p.r., lo cual como ya vimos recien no es cierto. El absurdo nos dice que \(T^{n,m}\) no es \((\Sigma\cup\Sigma_{p})\)-p.r..  

Proof. Por definicion \(T^{n,m}=M(Halt^{n,m})\).  

4.4.2.4 Uso de macros asociados a las funciones \(Halt^{n,m}\), \(E_{\#}^{n,m}\) y \(E_{\ast}^{n,m}\)

Aqui veremos, con ejemplos, como ciertos macros nos permitiran dentro de un programa hablar acerca del funcionamiento de otro programa. Esto junto con el hecho que cada funcion \(\Sigma\)-recursiva y cada predicado \(\Sigma\)-recursivo tienen su macro asociado (Corolario 4.3), sera muy util a la hora del diseño de programas y nos permitira simular dentro del paradigma imperativo muchas ideas usadas para el diseño de procedimientos efectivos. En este sentido la convinacion de los dos paradigmas (recursivo e imperativo) nos permite fortalecer notablemente al paradigma imperativo en su roll modelizador (o simulador) de los procedimientos efectivos. Esto es importante ya que el paradigma mas comodo, amplio e intuitivo, a la hora de decidir si algo es o no computable, es sin duda el filosofico o efectivo.

Veamos el primer ejemplo. Sea \(\Sigma=\{@,!\}\) y sea \(\mathcal{P}_{0}\in\mathrm{Pro}^{\Sigma}\) tal que \(0\in\mathrm{Dom}\Psi_{\mathcal{P}_{0}}^{1,0,\#}\) y \(\Psi_{\mathcal{P}_{0}}^{1,0,\#}(0)=2\). Probaremos que \[S=\{x\in\mathrm{Dom}\Psi_{\mathcal{P}_{0}}^{1,0,\#}:\Psi_{\mathcal{P}_{0}}^{1,0,\#}(x)\neq0\}\] es \(\Sigma\)-enumerable. Notese que \(0\in S\). Por definicion de conjunto \(\Sigma\)-enumerable, deberemos encontrar un programa \(\mathcal{P}\in\mathrm{Pro}^{\Sigma}\) tal que \(\mathrm{Dom}\Psi_{\mathcal{P}}^{1,0,\#}=\omega\) y \(\operatorname{Im}\Psi_{\mathcal{P}}^{1,0,\#}=S\). Dicho en palabras, el programa \(\mathcal{P}\) debera cumplir:

1. adhocprefix-adhocsufix siempre que lo corramos desde un estado de la forma \(\left\Vert x\right\Vert\), con \(x\in\omega\), debe detenerse y el contenido de la variable \(\mathrm{N}1\) bajo detencion debera ser un elemento de \(S\)

2. adhocprefix-adhocsufix para cada \(s\in S\) debera haber un \(x\in\omega\) tal que \(s\) es el valor de la variable \(\mathrm{N}1\) bajo detencion cuando corremos \(\mathcal{P}\) desde \(\left\Vert x\right\Vert\)

A continuacion daremos una descripcion intuitiva del funcionamiento de \(\mathcal{P}\) (pseudocodigo) para luego escribirlo correctamente usando macros. El programa \(\mathcal{P}\) comenzara del estado \(\left\Vert x\right\Vert\) y hara las siguientes tareas

1. adhocprefix adhocsufix Etapa 1: si \(x=0\) ir a Etapa 6, en caso contrario ir a Etapa 2.

2. adhocprefix adhocsufix Etapa 2: calcular \((x)_{1}\) y \((x)_{2}\) e ir a Etapa 3.

3. adhocprefix adhocsufix Etapa 3: si \(\mathcal{P}_{0}\) termina desde \(\left\Vert (x)_{1}\right\Vert\) en \((x)_{2}\) pasos ir a Etapa 4, en caso contrario ir a Etapa 6

4. adhocprefix adhocsufix Etapa 4: si el valor que queda en \(\mathrm{N}1\) luego de correr \(\mathcal{P}_{0}\) una cantidad \((x)_{2}\) de pasos, partiendo de \(\left\Vert (x)_{1}\right\Vert\), es distinto de 0, entonces ir a Etapa 5. En caso contrario ir a Etapa 6.

5. adhocprefix adhocsufix Etapa 5: asignar a \(\mathrm{N}1\) el valor \((x)_{1}\) y terminar

6. adhocprefix adhocsufix Etapa 6: asignar a \(\mathrm{N}1\) el valor \(0\) y terminar

Notese que la descripcion anterior no es ni mas ni menos que un procedimiento efectivo que enumera a \(S\), y nuestra mision es simularlo dentro del lenguaje \(\mathcal{S}^{\Sigma}\). Para esto usaremos varios macros. Ya que la funcion \(f=\lambda x[(x)_{1}]\) es \(\Sigma\)-p.r., el Corolario 4.3 nos dice que hay un macro: \[[\mathrm{V}2\leftarrow f(\mathrm{V}1)]\] el cual escribiremos de la siguiente manera mas intuitiva: \[[\mathrm{V}2\leftarrow(\mathrm{V}1)_{1}]\] Similarmente hay un macro: \[[\mathrm{V}2\leftarrow(\mathrm{V}1)_{2}]\] Tambien, ya que el predicado \(P=\lambda x[x=0]\) es \(\Sigma\)-recursivo, hay un macro: \[\left[\mathrm{IF}\;P(\mathrm{V}1)\;\mathrm{GOTO}\;\mathrm{A}1\right]\] el cual escribiremos de la siguiente manera: \[\left[\mathrm{IF}\;\mathrm{V}1=0\;\mathrm{GOTO}\;\mathrm{A}1\right]\] Definamos \[H=\lambda tx\left[Halt^{1,0}(t,x,\mathcal{P}_{0})\right]\] Notar que \(D_{H}=\omega^{2}\) y que \(H\) es \(\Sigma\)-mixta. Ademas sabemos que la funcion \(Halt^{1,0}\) es \((\Sigma\cup\Sigma_{p})\)-p.r. por lo cual resulta facilmente que \(H\) es \((\Sigma\cup\Sigma_{p})\)-p.r.. Por la Proposicion de Independencia del Alfabeto tenemos que \(H\) es \(\Sigma\)-p.r.. O sea que el Corolario 4.3 nos dice que hay un macro: \[\left[\mathrm{IF}\;H(\mathrm{V}1,\mathrm{V}2)\;\mathrm{GOTO}\;\mathrm{A}1\right]\] Para hacer mas intuitivo el uso de este macro lo escribiremos de la siguiente manera \[\left[\mathrm{IF}\;Halt^{1,0}(\mathrm{V}1,\mathrm{V}2,\mathcal{P}_{0})\;\mathrm{GOTO}\;\mathrm{A}1\right]\] Sea \[g=\lambda tx\left[E_{\#1}^{1,0}(t,x,\mathcal{P}_{0})\right]\] Ya que \(g\) es \(\Sigma\)-recursiva (por que?), hay un macro: \[\left[\mathrm{V}3\leftarrow g(\mathrm{V}1,\mathrm{V}2)\right]\] Para hacer mas intuitivo el uso de este macro lo escribiremos de la siguiente manera \[\left[\mathrm{V}3\leftarrow E_{\#1}^{1,0}(\mathrm{V}1,\mathrm{V}2,\mathcal{P}_{0})\right]\] Ahora si podemos dar nuestro progama \(\mathcal{P}\) que enumera a \(S\): \[\begin{array}{ll} & \mathrm{IF}\;\mathrm{N}1\neq0\;\mathrm{GOTO}\;\mathrm{L}1\\ & \mathrm{GOTO}\;\mathrm{L}2\\ \mathrm{L}1 & [\mathrm{N}3\leftarrow(\mathrm{N}1)_{1}]\\ & [\mathrm{N}4\leftarrow(\mathrm{N}1)_{2}]\\ & \left[\mathrm{IF}\;Halt^{1,0}(\mathrm{N}4,\mathrm{N}3,\mathcal{P}_{0})\;\mathrm{GOTO}\;\mathrm{L}3\right]\\ & \mathrm{GOTO}\;\mathrm{L}2\\ \mathrm{L}3 & \left[\mathrm{N}5\leftarrow E_{\#1}^{1,0}(\mathrm{N}4,\mathrm{N}3,\mathcal{P}_{0})\right]\\ & [\mathrm{IF}\;\mathrm{N}5=0\;\mathrm{GOTO}\;\mathrm{L}2]\\ & \mathrm{N}1\leftarrow\mathrm{N}3\\ & \mathrm{GOTO}\;\mathrm{L}4\\ \mathrm{L}2 & \mathrm{N}1\leftarrow0\\ \mathrm{L}4 & \mathrm{SKIP} \end{array}\]

Enumeracion de conjuntos de programas

Ya que los programas de \(\mathcal{S}^{\Sigma}\) son palabras del alfabeto \(\Sigma\cup\Sigma_{p}\), nos podemos preguntar cuando un conjunto \(L\) de programas es \((\Sigma\cup\Sigma_{p})\)-enumerable. Daremos un ejemplo. Sea \(\Sigma=\{@,!\}\) y sea \[L=\{\mathcal{P}\in\mathrm{Pro}^{\Sigma}:\Psi_{\mathcal{P}}^{1,0,\#}(10)=10\}\] Veremos que \(L\) es \((\Sigma\cup\Sigma_{p})\)-enumerable, dando un programa \(\mathcal{Q}\in\mathrm{Pro}^{\Sigma\cup\Sigma_{p}}\) que enumere a \(L\), es decir tal que Dom\((\Psi_{\mathcal{Q}}^{1,0,\ast})=\omega\) y \(\operatorname{Im}(\Psi_{\mathcal{Q}}^{1,0,\ast})=L\). Cabe destacar que aqui hay en juego dos versiones de nuestro lenguaje imperativo, es decir enumeraremos un conjunto de programas de \(\mathcal{S}^{\Sigma}\) usando un programa de \(\mathcal{S}^{\Sigma\cup\Sigma_{p}}\). Sea \(\leq\) un orden total sobre el conjunto \(\Sigma\cup\Sigma_{p}\).

A continuacion daremos una descripcion intuitiva del funcionamiento de \(\mathcal{Q}\) (pseudocodigo) para luego escribirlo correctamente usando macros. Notese que \(\mathrm{SKIP}\in L\). El programa \(\mathcal{Q}\) comenzara del estado \(\left\Vert x\right\Vert\) y hara las siguientes tareas

1. adhocprefix adhocsufix Etapa 1: si \(x=0\) ir a Etapa 6, en caso contrario ir a Etapa 2.

2. adhocprefix adhocsufix Etapa 2: calcular \((x)_{1}\), \((x)_{2}\) y \(\ast^{\leq}((x)_{1})\) e ir a Etapa 3.

3. adhocprefix adhocsufix Etapa 3: si \(\ast^{\leq}((x)_{1})\in\mathrm{Pro}^{\Sigma}\) y termina partiendo desde \(\left\Vert 10\right\Vert\) en \((x)_{2}\) pasos ir a Etapa 4, en caso contrario ir a Etapa 6

4. adhocprefix adhocsufix Etapa 4: si el valor que queda en \(\mathrm{N}1\) luego de correr \(\ast^{\leq}((x)_{1})\) una cantidad \((x)_{2}\) de pasos, partiendo de \(\left\Vert 10\right\Vert\) es igual a 10, entonces ir a Etapa 5. En caso contrario ir a Etapa 6.

5. adhocprefix adhocsufix Etapa 5: asignar a \(\mathrm{P}1\) la palabra \(\ast^{\leq}((x)_{1})\) y terminar

6. adhocprefix adhocsufix Etapa 6: asignar a \(\mathrm{P}1\) la palabra \(\mathrm{SKIP}\) y terminar

Notese que la descripcion anterior no es ni mas ni menos que un procedimiento efectivo que enumera a \(L\), y nuestra mision es simularlo dentro del lenguaje \(\mathcal{S}^{\Sigma\cup\Sigma_{p}}\). Para esto usaremos varios macros. Es importante notar que los macros que usaremos corresponden al lenguaje \(\mathcal{S}^{\Sigma\cup\Sigma_{p}}\) ya que los usaremos en \(\mathcal{Q}\) el cual sera un programa de \(\mathcal{S}^{\Sigma\cup\Sigma_{p}}\).

Ya que las funciones \(\lambda x[(x)_{1}]\) y \(\lambda x[(x)_{2}]\) son \((\Sigma\cup\Sigma_{p})\)-recursivas el Corolario 4.3 nos dice que hay macros asociados a estas funciones los cuales escribiremos de la siguiente manera mas intuitiva: \[\begin{aligned} \\{} [\mathrm{V}2 & \leftarrow(\mathrm{V}1)_{2}] \end{aligned}\] Ya que el predicado \(P=\lambda x[x=10]\) es \((\Sigma\cup\Sigma_{p})\)-recursivo tenemos su macro asociado el cual escribiremos de la siguiente manera: \[\left[\mathrm{IF}\;\mathrm{V}1=10\;\mathrm{GOTO}\;\mathrm{A}1\right]\] Por un lema anterior sabemos que \(\mathrm{Pro}^{\Sigma}\) es un conjunto \((\Sigma\cup\Sigma_{p})\)-p.r., por lo cual \(\chi_{\mathrm{Pro}^{\Sigma}}^{(\Sigma\cup\Sigma_{p})^{\ast}}\) es \((\Sigma\cup\Sigma_{p})\)-p.r., por lo cual hay un macro \[\left[\mathrm{IF}\;\chi_{\mathrm{Pro}^{\Sigma}}^{(\Sigma\cup\Sigma_{p})^{\ast}}(\mathrm{W}1)\;\mathrm{GOTO}\;\mathrm{A}1\right]\] el cual escribiremos de la siguiente manera \[\left[\mathrm{IF}\;\mathrm{W}1\in\mathrm{Pro}^{\Sigma}\;\mathrm{GOTO}\;\mathrm{A}1\right]\] Ya que el predicado \(Halt^{1,0}\) es \((\Sigma\cup\Sigma_{p})\)-recursivo tenemos un macro asociado a el, el cual escribiremos de la siguiente forma \[\left[\mathrm{IF}\;Halt^{1,0}(\mathrm{V}1,\mathrm{V}2,\mathrm{W}1)\;\mathrm{GOTO}\;\mathrm{A}1\right]\] Ya que \(E_{\#1}^{1,0}\) es \((\Sigma\cup\Sigma_{p})\)-recursivo tenemos un macro asociado a ella, el cual escribiremos de la siguiente forma \[\left[\mathrm{V}3\leftarrow E_{\#1}^{1,0}(\mathrm{V}1,\mathrm{V}2,\mathrm{W}1)\right]\] Tambien usaremos macros \[\begin{gathered} \\ \left[\mathrm{W}1\leftarrow\mathrm{SKIP}\right] \end{gathered}\] (dejamos al lector hacerlos a mano o tambien se puede justificar su existencia via la proposicion de existencia de macros aplicada a las funciones \(C_{10}^{0,0}\) y \(C_{\mathrm{SKIP}}^{0,0}\)).

Ahora si podemos hacer el programa \(\mathcal{Q}\) que enumera a \(L\): \[\begin{array}{ll} & \mathrm{IF}\;\mathrm{N}1\neq0\;\mathrm{GOTO}\;\mathrm{L}1\\ & \mathrm{GOTO}\;\mathrm{L}2\\ \mathrm{L}1 & [\mathrm{N}2\leftarrow(\mathrm{N}1)_{1}]\\ & [\mathrm{N}3\leftarrow(\mathrm{N}1)_{2}]\\ & [\mathrm{P}1\leftarrow\ast^{\leq}(\mathrm{N}2)]\\ & \left[\mathrm{IF}\;\mathrm{P}1\in\mathrm{Pro}^{\Sigma}\;\mathrm{GOTO}\;\mathrm{L}3\right]\\ & \mathrm{GOTO}\;\mathrm{L}2\\ \mathrm{L}3 & [\mathrm{N}4\leftarrow10]\\ & \left[\mathrm{IF}\;Halt^{1,0}(\mathrm{N}3,\mathrm{N}4,\mathrm{P}1)\;\mathrm{GOTO}\;\mathrm{L}4\right]\\ & \mathrm{GOTO}\;\mathrm{L}2\\ \mathrm{L}4 & \left[\mathrm{N}5\leftarrow E_{\#1}^{1,0}(\mathrm{N}3,\mathrm{N}4,\mathrm{P}1)\right]\\ & [\mathrm{IF}\;\mathrm{N}5=10\;\mathrm{GOTO}\;\mathrm{L}4]\\ \mathrm{L}2 & \left[\mathrm{P}1\leftarrow\mathrm{SKIP}\right]\\ \mathrm{L}4 & \mathrm{SKIP} \end{array}\]

Cuando \(\Sigma\supseteq\Sigma_{p}\) podemos correr un programa \(\mathcal{P}\in\mathrm{Pro}^{\Sigma}\) partiendo de un estado que asigne a sus variables alfabeticas programas (ya que los programas son meras palabras de \(\Sigma^{\ast}\)). En particular podriamos correr un programa \(\mathcal{P}\) desde el estado \(\left\Vert \mathcal{P}\right\Vert\). Llamaremos \(A\) al conjunto formado por aquellos programas \(\mathcal{P}\) tales que \(\mathcal{P}\) se detiene partiendo del estado \(\left\Vert \mathcal{P}\right\Vert\). Es decir \[A=\{\mathcal{P}\in\mathrm{Pro}^{\Sigma}:\exists t\in\omega\text{ tal que }Halt^{0,1}(t,\mathcal{P},\mathcal{P})=1\}\] Por ejemplo \(\mathrm{SKIP}\in A\). Dicho rapida y sugestivamente \(A\) es el conjunto formado por aquellos programas que se detienen partiendo de si mismos. Dejamos al lector hacer un programa que enumere a \(A\). Como veremos mas adelante este conjunto, si bien es \(\Sigma\)-enumerable, no es \(\Sigma\)-computable.

4.4.3 Godel vence a Turing

Para probar que toda funcion \(\Sigma\)-Turing computable es \(\Sigma\)-recursiva debemos estudiar la recursividad del funcionamiento de las maquinas de Turing. Cabe destacar que tal como se lo explico en la Subseccion [BasicosMaquinasDeTuring] supondremos siempre que el conjunto de estados de una maquina de Turing \(M=\left(Q,\Sigma,\Gamma,\delta,q_{0},B,F\right)\) es un alfabeto disjunto con \(\Gamma\).

Primero probaremos algunos lemas basicos.

Notese que la funcion \(\delta\) de una maquina de Turing \(M=\left(Q,\Sigma,\Gamma,\delta,q_{0},B,F\right)\) no es \((\Gamma\cup Q)\)-mixta. Sin envargo los siguientes predicados \((\Gamma\cup Q)\)-mixtos contienen toda la informacion de \(\delta\): \[\begin{array}{rcl} P_{L}:Q\times\Gamma\times Q\times\Gamma & \rightarrow & \omega\\ (p,\sigma,q,\gamma) & \rightarrow & \left\{ \begin{array}{ccl} 1 & & \text{si }\delta(q,\gamma)=(p,\sigma,L)\\ 0 & & \text{caso contrario} \end{array}\right. \end{array}\] \[\begin{array}{rcl} P_{L}:Q\times\Gamma\times Q\times\Gamma & \rightarrow & \omega\\ (p,\sigma,q,\gamma) & \rightarrow & \left\{ \begin{array}{ccl} 1 & & \text{si }(p,\sigma,L)\in\delta(q,\gamma)\\ 0 & & \text{caso contrario} \end{array}\right. \end{array}\] \[\begin{array}{rcl} P_{R}:Q\times\Gamma\times Q\times\Gamma & \rightarrow & \omega\\ (p,\sigma,q,\gamma) & \rightarrow & \left\{ \begin{array}{ccl} 1 & & \text{si }\delta(q,\gamma)=(p,\sigma,R)\\ 0 & & \text{caso contrario} \end{array}\right. \end{array}\] \[\begin{array}{rcl} P_{K}:Q\times\Gamma\times Q\times\Gamma & \rightarrow & \omega\\ (p,\sigma,q,\gamma) & \rightarrow & \left\{ \begin{array}{ccl} 1 & & \text{si }\delta(q,\gamma)=(p,\sigma,K)\\ 0 & & \text{caso contrario} \end{array}\right. \end{array}\]

Proof. Ya que los tres predicados tienen dominio finito, el Corolario 4.2 nos dice que son \((\Gamma\cup Q)\)-p.r.  

Recordemos que dado \(\alpha\in(Q\cup\Gamma)^{\ast}\), definimos \(\left\lfloor \alpha\right\rfloor\) de la siguiente manera \[\begin{aligned} \left\lfloor \varepsilon\right\rfloor & =\varepsilon\\ \left\lfloor \alpha\sigma\right\rfloor & =\alpha\sigma\text{, si }\sigma\neq B\\ \left\lfloor \alpha B\right\rfloor & =\left\lfloor \alpha\right\rfloor \end{aligned}\] Es decir \(\left\lfloor \alpha\right\rfloor\) es el resultado de remover de \(\alpha\) el tramo final mas grande de la forma \(B^{n}\).

Tambien dada cualquier palabra \(\alpha\) definimos \[\begin{aligned} ^{\curvearrowright}\alpha & =\left\{ \begin{array}{lll} \left[\alpha\right]_{2}...\left[\alpha\right]_{\left\vert \alpha\right\vert } & \text{si} & \left\vert \alpha\right\vert \geq2\\ \varepsilon & \text{si} & \left\vert \alpha\right\vert \leq1 \end{array}\right.\\ \alpha^{\curvearrowleft} & =\left\{ \begin{array}{lll} \left[\alpha\right]_{1}...\left[\alpha\right]_{\left\vert \alpha\right\vert -1} & \text{si} & \left\vert \alpha\right\vert \geq2\\ \varepsilon & \text{si} & \left\vert \alpha\right\vert \leq1 \end{array}\right. \end{aligned}\]

Notese que dada una maquina de Turing \(M\), la expresion \(d\underset{M}{\vdash}d^{\prime}\) fue definida solo en el caso en que \(d\) y \(d^{\prime}\) son descripciones instantaneas. Es decir que el predicado \(\lambda dd^{\prime}\left[d\vdash d^{\prime}\right]\) tiene dominio igual a \(Des\times Des\).

Proof. Sea \(\tilde{P}_{L}:Des\times Des\times\Gamma\times\Gamma^{\ast}\times\Gamma^{\ast}\times Q\times Q\rightarrow\omega\) definido por \(\tilde{P}_{L}(d,d^{\prime},\sigma,\alpha,\beta,p,q)=1\) sii \[d=\alpha p\beta\wedge(q,\sigma,L)=\delta\left(p,\left[\beta B\right]_{1}\right)\wedge\alpha\neq\varepsilon\wedge d^{\prime}=\left\lfloor \alpha^{\curvearrowleft}q\left[\alpha\right]_{\left\vert \alpha\right\vert }\sigma^{\curvearrowright}\beta\right\rfloor\] Sea \(\tilde{P}_{R}:Des\times Des\times\Gamma\times\Gamma^{\ast}\times\Gamma^{\ast}\times Q\times Q\rightarrow\omega\) definido por \(\tilde{P}_{R}(d,d^{\prime},\sigma,\alpha,\beta,p,q)=1\) sii \[d=\alpha p\beta\wedge(q,\sigma,R)=\delta\left(p,\left[\beta B\right]_{1}\right)\wedge d^{\prime}=\alpha\sigma q^{\curvearrowright}\beta\] Sea \(\tilde{P}_{K}:Des\times Des\times\Gamma\times\Gamma^{\ast}\times\Gamma^{\ast}\times Q\times Q\rightarrow\omega\) definido por \(\tilde{P}_{K}(d,d^{\prime},\sigma,\alpha,\beta,p,q)=1\) sii \[d=\alpha p\beta\wedge(q,\sigma,K)=\delta\left(p,\left[\beta B\right]_{1}\right)\wedge d^{\prime}=\left\lfloor \alpha q\sigma^{\curvearrowright}\beta\right\rfloor\] Se deja al lector la verificacion de que estos predicados son \((\Gamma\cup Q)\)-p.r.. Notese que \(\lambda dd^{\prime}\left[d\underset{M}{\vdash}d^{\prime}\right]\) es igual al predicado \[\lambda dd^{\prime}\left[(\exists\sigma\in\Gamma)(\exists\alpha,\beta\in\Gamma^{\ast})(\exists p,q\in Q)(\tilde{P}_{R}\vee\tilde{P}_{L}\vee\tilde{P}_{K})(d,d^{\prime},\sigma,\alpha,\beta,p,q)\right]\] lo cual por el Lema 4.21 nos dice que \(\lambda dd^{\prime}\left[d\underset{M}{\vdash}d^{\prime}\right]\) es \((\Gamma\cup Q)\)-p.r.  

Proof. Sea \(Q=\lambda dd^{\prime}\left[d\underset{M}{\vdash}d^{\prime}\right]\cup C_{0}^{0,2}|_{(\Gamma\cup Q)^{\ast2}-Des^{2}}\) es decir \(Q\) es el resultado de extender con el valor \(0\) al predicado \(\lambda dd^{\prime}\left[d\underset{M}{\vdash}d^{\prime}\right]\) de manera que este definido en todo \((\Gamma\cup Q)^{\ast2}\). Sea \(\leq\) un orden total sobre \(\Gamma\cup Q\) y sea \(Q_{1}:\mathbf{N}\times Des\times Des\rightarrow\omega\) definido por \(Q_{1}(x,d,d^{\prime})=1\) sii  

\(\left((\forall i\in\mathbf{N})_{i\leq Lt(x)}\ast^{\leq}((x)_{i})\in Des\right)\wedge\ast^{\leq}((x)_{1})=d\wedge\)

\(\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ast^{\leq}((x)_{Lt(x)})=d^{\prime}\wedge\left((\forall i\in\mathbf{N})_{i\leq Lt(x)\dot{-}1}\;Q(\ast^{\leq}((x)_{i}),\ast^{\leq}((x)_{i+1}))\right)\)

Notese que dicho rapidamente \(Q_{1}(x,d,d^{\prime})=1\) sii \(x\) codifica una computacion que parte de \(d\) y llega a \(d^{\prime}\). Se deja al lector la verificacion de que este predicado es \((\Gamma\cup Q)\)-p.r.. Notese que \[\lambda ndd^{\prime}\left[d\underset{M}{\overset{n}{\vdash}}d^{\prime}\right]=\lambda ndd^{\prime}\left[\left(\exists x\in\mathbf{N}\right)\;Lt(x)=n+1\wedge Q_{1}(x,d,d^{\prime})\right]\] Es decir que solo nos falta acotar el cuantificador existencial, para poder aplicar el lema de cuantificacion acotada. Ya que cuando \(d_{1},...,d_{n+1}\in Des\) son tales que \(d_{1}\underset{M}{\vdash}d_{2}\underset{M}{\vdash}\cdots\underset{M}{\vdash}d_{n+1}\) tenemos que \[\left\vert d_{i}\right\vert \leq\left\vert d_{1}\right\vert +n\text{, para }i=1,...,n\] una posible cota para dicho cuantificador es \[\prod_{i=1}^{n+1}pr(i)^{\left\vert \Gamma\cup Q\right\vert ^{\left\vert d\right\vert +n}}\text{.}\] O sea que, por el lema de cuantificacion acotada, tenemos que el predicado \(\lambda ndd^{\prime}\left[d\underset{M}{\overset{n}{\vdash}}d^{\prime}\right]\) es \((\Gamma\cup Q)\)-p.r.

Proof. Supongamos \(O=\Sigma^{\ast}\) y sea \(M=\left(Q,\Sigma,\Gamma,\delta,q_{0},B,\shortmid,F\right)\) una maquina de Turing con unit la cual compute a \(f\). Sea \(\leq\) un orden total sobre \(\Sigma\). Notese que por el Teorema 4.2, la funcion \(\ast^{\leq}\) es \((\Gamma\cup Q)\)-p.r.. Sea \(P:\mathbf{N}\times\omega^{n}\times\Sigma^{\ast m}\rightarrow\omega\) dado por \(P(x,\vec{x},\vec{\alpha})=1\) sii  

1. \((\exists q\in Q)\;\left\lfloor q_{0}B\shortmid^{x_{1}}...B\shortmid^{x_{n}}B\alpha_{1}...B\alpha_{m}\right\rfloor \underset{M}{\overset{(x)_{1}}{\vdash}}\left\lfloor qB\ast^{\leq}((x)_{2})\right\rfloor \wedge\)

2. \(\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \wedge(\forall d\in Des)_{\left\vert d\right\vert \leq\left\vert \ast^{\leq}((x)_{2})\right\vert +2}\;\lnot\left(\left\lfloor qB\ast^{\leq}((x)_{2})\right\rfloor \underset{M}{\vdash}d\right)\)

Dejamos al lector la prueba de que \(P\) es \((\Gamma\cup Q)\)-p.r.. Ya que \(P\) es \(\Sigma\)-mixto, el Teorema 4.2 nos dice que \(P\) es \(\Sigma\)-p.r.. Notese que \[f=\lambda\vec{x}\vec{\alpha}\left[\ast^{\leq}\left(\left(\min_{x}P(x,\vec{x},\vec{\alpha})\right)_{2}\right)\right]\text{,}\] lo cual nos dice que \(f\) es \(\Sigma\)-recursiva.

4.4.4 Turing vence a Neumann

Probaremos que toda funcion \(\Sigma\)-computable es \(\Sigma\)-Turing computable. Para esto probaremos un resultado general que nos enseñara a simular el comportamiento de un programa con una maquina de Turing. Es importante notar que la simulacion que nos interesa que haga la maquina simuladora no es a nivel de la funcion que computa el programa sino a un nivel mas general, es decir nos interesa que simule a dicho programa como transformador de estados. En particular y usada adecuadamente, la maquina simuladora nos servira para confeccionar una maquina que compute una funcion computada por un programa dado.

4.4.4.1 Construccion de la maquina simuladora de un programa

Dado \(\mathcal{P}\in\mathrm{Pro}^{\Sigma}\), definamos \[\begin{aligned} N(\mathcal{P}) & =\mathrm{menor}\ k\in\mathbf{N}\ \mathrm{tal\ que\ las\ variables\ que\ ocurren\ en\ }\mathcal{P}\\ & \mathrm{esta}\text{n}\mathrm{\ todas\ en\ la\ lista\ N}1,...,\mathrm{N}\bar{k},\mathrm{P}1,...,\mathrm{P}\bar{k} \end{aligned}\] Por ejemplo si \(\mathcal{P}\) es el siguiente programa (aqui \(\Sigma=\{\blacktriangle,\#\}\)) \[\begin{array}{ll} \mathrm{L}1 & \mathrm{N}4\leftarrow\mathrm{N}4+1\\ & \mathrm{P}1\leftarrow\mathrm{P}1.\blacktriangle\\ & \mathrm{IF\ N}1\neq0\ \mathrm{GOTO}\;\mathrm{L}1 \end{array}\] entonces tenemos \(N(\mathcal{P})=4\)

Sea \(\mathcal{P}\) un programa y sea \(k\) fijo y mayor o igual a \(N(\mathcal{P})\). La construccion de la maquina simuladora dependera de \(\mathcal{P}\) y de \(k\). Notese que cuando \(\mathcal{P}\) se corre desde algun estado de la forma \[\left\Vert x_{1},...,x_{k},\alpha_{1},...,\alpha_{k}\right\Vert\] los sucesivos estados por los que va pasando son todos de la forma \[\left\Vert y_{1},...,y_{k},\beta_{1},...,\beta_{k}\right\Vert\] es decir en todos ellos las variables con indice mayor que \(k\) valen \(0\) o \(\varepsilon\). La razon es simple: ya que en \(\mathcal{P}\) no figuran las variables \[\begin{aligned} & \mathrm{N}\overline{k+1},\mathrm{N}\overline{k+2},...\\ & \mathrm{P}\overline{k+1},\mathrm{P}\overline{k+2},... \end{aligned}\] estas variables quedan con valores \(0\) y \(\varepsilon\), respectivamente a lo largo de toda la computacion.

La maquina simuladora que construiremos simulara a \(\mathcal{P}\) en cuanto a su funcionamiento cuando partimos de estados de la forma \(\left\Vert x_{1},...,x_{k},\alpha_{1},...,\alpha_{k}\right\Vert\). Necesitaremos tener alguna manera de representar en la cinta los diferentes estados por los cuales se va pasando, a medida que corremos a \(\mathcal{P}\). Esto lo haremos de la siguiente forma: al estado \[\left\Vert x_{1},...,x_{k},\alpha_{1},...,\alpha_{k}\right\Vert\] lo representaremos en la cinta de la siguiente manera \[B\shortmid^{x_{1}}...B\shortmid^{x_{k}}B\alpha_{1}...B\alpha_{k}BBBB....\] Por ejemplo consideremos el programa \(\mathcal{P}\) mostrado recien y fijemos \(k=6\). Entonces al estado \[\left\Vert 3,2,5,0,4,2,\blacktriangle,\blacktriangle\blacktriangle,\varepsilon,\#\blacktriangle,\#,\#\#\#\right\Vert\] lo representaremos en la cinta de la siguiente manera \[B\mathrm{\shortmid\shortmid\shortmid}B\mathrm{\shortmid\shortmid}B\mathrm{\shortmid\shortmid\shortmid\shortmid\shortmid}BB\mathrm{\shortmid\shortmid\shortmid\shortmid}B\mathrm{\shortmid\shortmid}B\blacktriangle B\blacktriangle\blacktriangle BB\#\blacktriangle B\#B\#\#\#BBBBB....\] A lo que queda entre dos blancos consecutivos (es decir que no hay ningun blanco entre ellos) lo llamaremos "bloque", por ejemplo en la cinta de arriba tenemos que los primeros 12 bloques son \[\shortmid\shortmid\shortmid\ \ \ \shortmid\shortmid\ \ \ \shortmid\shortmid\shortmid\shortmid\shortmid\ \ \ \ \varepsilon\ \ \ \ \shortmid\shortmid\shortmid\shortmid\ \ \ \shortmid\shortmid\ \ \ \blacktriangle\ \ \ \ \ \blacktriangle\blacktriangle\ \ \ \ \ \varepsilon\ \ \ \ \ \#\blacktriangle\ \ \ \ \ \#\ \ \ \ \ \#\#\#\] y despues los bloques siguientes (que son infinitos ya que la cinta es infinita hacia la derecha) son todos iguales a \(\varepsilon\).

Una observacion importante es que esta forma de representacion de estados en la cinta depende del \(k\) elejido, es decir si tomaramos otro \(k\), por ejemplo \(k=9\), entonces el estado anterior se representaria de otra forma en la cinta. Aqui se ve claramente que la maquina simuladora que construiremos dependera del \(k\) elejido.

4.4.4.1.1 Construccion de las maquinas simuladoras de instrucciones

Armaremos la maquina simuladora como concatenacion de maquinas las cuales simularan, via la representacion anterior, el funcionamiento de las distintas instrucciones de \(\mathcal{P}\). Asumiremos que en \(\mathcal{P}\) no hay instrucciones de la forma \(\mathrm{GOTO}\;\mathrm{L}\bar{m}\) ni de la forma \(\mathrm{L}\bar{n}\ \mathrm{GOTO}\;\mathrm{L}\bar{m}\). Esto simplificara un poco la construccion de la maquina simuladora y de hecho lo podemos hacer ya que toda funcion \(\Sigma\)-computable puede ser computada por un programa sin este tipo de instrucciones, tal como lo veremos mas adelante (Lema 4.53).

Para poder hacer concretamente las maquinas simuladoras de instrucciones deberemos diseñar antes algunas maquinas auxiliares. Todas las maquinas descriptas a continuacion tendran a \(\shortmid\) como unit y a \(B\) como blanco, tendran a \(\Sigma\) como su alfabeto terminal y su alfabeto mayor sera \(\Gamma=\Sigma\cup\{B,\shortmid\}\cup\{\tilde{a}:a\in\Sigma\cup\{\shortmid\}\}\). Ademas tendran uno o dos estados finales con la propiedad de que si \(q\) es un estado final, entonces \((q,\sigma)\notin D_{\delta}\), para cada \(\sigma\in\Gamma\).

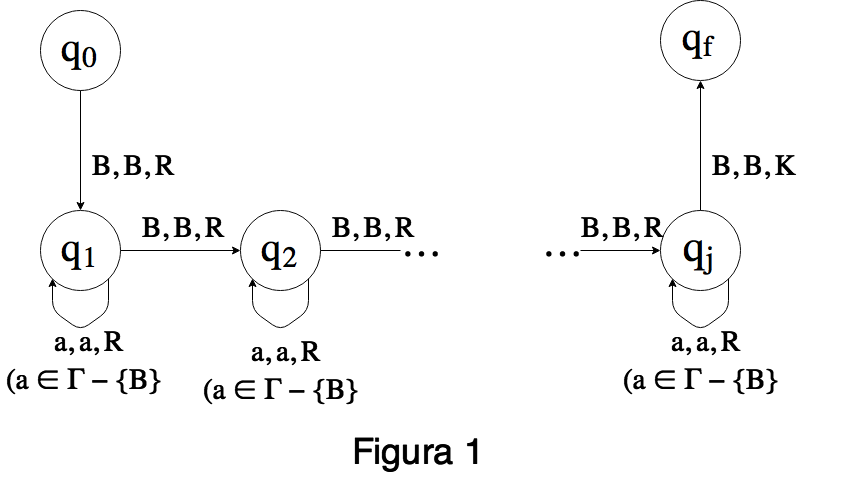
Para cada \(j\geq1\), sea \(D_{j}\) la siguiente maquina:

@@figura:figure1.png@@

Notese que \[\begin{array}{lcr} \alpha B\beta_{1}B\beta_{2}B...B\beta_{j}B\gamma & \overset{\ast}{\vdash} & \alpha B\beta_{1}B\beta_{2}B...B\beta_{j}B\gamma\\ \ \ \uparrow & & \uparrow\ \ \\ \ \ q_{0} & & q_{f}\ \ \end{array}\] siempre que \(\alpha,\gamma\in\Gamma^{\ast}\), \(\beta_{1},...,\beta_{j}\in(\Gamma-\{B\})^{\ast}\). Es decir la maquina \(D_{j}\) lo unico que hace es mover el cabezal desde el blanco de la izquierda de un bloque determinado, exactamente \(j\) bloques a la derecha

Analogamente \(I_{j}\) sera una maquina que desplaza el cabezal \(j\) bloques a la izquierda del blanco que esta escaneando. Es decir \(I_{j}\) cumplira que \[\begin{array}{lcr} \alpha B\beta_{j}B...B\beta_{2}B\beta_{1}B\gamma & \overset{\ast}{\vdash} & \alpha B\beta_{j}B...B\beta_{2}B\beta_{1}B\gamma\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \uparrow & & \uparrow\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ q_{0} & & q_{f}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \end{array}\] siempre que \(\alpha,\gamma\in\Gamma^{\ast}\), \(\beta_{1},...,\beta_{j}\in(\Gamma-\{B\})^{\ast}\). Dejamos al lector la manufactura de esta maquina.

Para \(j\geq1\), sea \(TD_{j}\) una maquina con un solo estado final \(q_{f}\) y tal que \[\begin{array}{ccc} \alpha B\gamma & \overset{\ast}{\vdash} & \alpha BB\gamma\\ \uparrow & & \uparrow\ \ \\ q_{0} & & q_{f}\ \ \end{array}\] cada vez que \(\alpha,\gamma\in\Gamma^{\ast}\) y \(\gamma\) tiene exactamente \(j\) ocurrencias de \(B\). Es decir la maquina \(TD_{j}\) corre un espacio a la derecha todo el segmento \(\gamma\) y agrega un blanco en el espacio que se genera a la izquierda. Por ejemplo, para el caso de \(\Sigma=\{a\}\) podemos tomar \(TD_{3}\) igual a la siguiente maquina:

@@figura:figure2.png@@

Analogamente, para \(j\geq1\), sea \(TI_{j}\) una maquina tal que \[\begin{array}{ccc} \alpha B\sigma\gamma & \overset{\ast}{\vdash} & \alpha B\gamma\\ \uparrow\ & & \uparrow\\ q_{0}\ \ & & q_{f} \end{array}\] cada vez que \(\alpha\in\Gamma^{\ast}\), \(\sigma\in\Gamma\) y \(\gamma\) tiene exactamente \(j\) ocurrencias de \(B\). Es decir la maquina \(TI_{j}\) corre un espacio a la izquierda todo el segmaneto \(\gamma\) (por lo cual en el lugar de \(\sigma\) queda el primer simbolo de \(\gamma\)). Dejamos al lector la construccion de por ejemplo \(TI_{3}\) para \(\Sigma=\{a\}\).

A continuacion describiremos las distintas maquinas simuladoras de instrucciones (y para algunos casos mostraremos concretamente como pueden ser hechas usando las maquinas anteriores).

Para \(1\leq i\leq k\), sea \(M_{i,k}^{+}\) una maquina tal que cualesquiera sean \(x_{1},...,x_{k}\in\omega\) y \(\alpha_{1},...,\alpha_{k}\in\Sigma^{\ast}\): \[\begin{array}{lcl} B\shortmid^{x_{1}}...B\shortmid^{x_{k}}B\alpha_{1}...B\alpha_{k} & \overset{\ast}{\vdash} & B\shortmid^{x_{1}}...B\shortmid^{x_{i-1}}B\shortmid^{x_{i}+1}B\shortmid^{x_{i+1}}...B\shortmid^{x_{k}}B\alpha_{1}...B\alpha_{k}\\ \uparrow & & \uparrow\\ q_{0} & & q_{f} \end{array}\] donde \(q_{0}\) es el estado inicial y \(q_{f}\) es el unico estado final de \(M_{i,k}^{+}\). Es claro que la maquina \(M_{i,k}^{+}\) simula la instruccion \(\mathrm{N}\bar{\imath}\leftarrow\mathrm{N}\bar{\imath}+1\), via la representacion de estados en la cinta con respecto a \(k\).

Para \(1\leq i\leq k\), sea \(M_{i,k}^{\dot{-}}\) una maquina tal que cualesquiera sean \(x_{1},...,x_{k}\in\omega\) y \(\alpha_{1},...,\alpha_{k}\in\Sigma^{\ast}\): \[\begin{array}{lcl} B\shortmid^{x_{1}}...B\shortmid^{x_{k}}B\alpha_{1}...B\alpha_{k} & \overset{\ast}{\vdash} & B\shortmid^{x_{1}}...B\shortmid^{x_{i-1}}B\shortmid^{x_{i}\dot{-}1}B\shortmid^{x_{i+1}}...B\shortmid^{x_{k}}B\alpha_{1}...B\alpha_{k}\\ \uparrow & & \uparrow\\ q_{0} & & q_{f} \end{array}\] donde \(q_{0}\) es el estado inicial y \(q_{f}\) es el unico estado final de \(M_{i,k}^{\dot{-}}\). Es claro que la maquina \(M_{i,k}^{\dot{-}}\) simula la instruccion \(\mathrm{P}\bar{\imath}\leftarrow\mathrm{P}\bar{\imath}\dot{-}1\), via la representacion de estados en la cinta con respecto a \(k\).

Para \(1\leq i\leq k\) y \(a\in\Sigma\), sea \(M_{i,k}^{a}\) una maquina tal que cualesquiera sean \(x_{1},...,x_{k}\in\omega\) y \(\alpha_{1},...,\alpha_{k}\in\Sigma^{\ast}\): \[\begin{array}{lcl} B\shortmid^{x_{1}}...B\shortmid^{x_{k}}B\alpha_{1}...B\alpha_{k} & \overset{\ast}{\vdash} & B\shortmid^{x_{1}}...B\shortmid^{x_{k}}B\alpha_{1}...B\alpha_{i-1}B\alpha_{i}aB\alpha_{i+1}...B\alpha_{k}\\ \uparrow & & \uparrow\\ q_{0} & & q_{f} \end{array}\] donde \(q_{0}\) es el estado inicial y \(q_{f}\) es el unico estado final de \(M_{i,k}^{a}\). Es claro que la maquina \(M_{i,k}^{a}\) simula la instruccion \(\mathrm{P}\bar{\imath}\leftarrow\mathrm{P}\bar{\imath}.a\), via la representacion de estados en la cinta con respecto a \(k\). La maquina \(M_{i,k}^{a}\).puede hacerse de la siguiente manera:

@@figura:figure3.png@@

Para \(1\leq i\leq k\), sea \(M_{i,k}^{\curvearrowright}\) una maquina tal que cualesquiera sean \(x_{1},...,x_{k}\in\omega\) y \(\alpha_{1},...,\alpha_{k}\in\Sigma^{\ast}\): \[\begin{array}{lcl} B\shortmid^{x_{1}}...B\shortmid^{x_{k}}B\alpha_{1}...B\alpha_{k} & \overset{\ast}{\vdash} & B\shortmid^{x_{1}}...B\shortmid^{x_{k}}B\alpha_{1}...B\alpha_{i-1}B^{\curvearrowright}\alpha_{i}B\alpha_{i+1}...B\alpha_{k}\\ \uparrow & & \uparrow\\ q_{0} & & q_{f} \end{array}\] donde \(q_{0}\) es el estado inicial y \(q_{f}\) es el unico estado final de \(M_{i,k}^{\curvearrowright}\). Es claro que la maquina \(M_{i,k}^{\curvearrowright}\) simula la instruccion \(\mathrm{P}\bar{\imath}\leftarrow\ ^{\curvearrowright}\mathrm{P}\bar{\imath}\), via la representacion de estados en la cinta con respecto a \(k\).

Para \(1\leq i,j\leq k\), sea \(M_{i\leftarrow j}^{\#,k}\) una maquina tal que cualesquiera sean \(x_{1},...,x_{k}\in\omega\) y \(\alpha_{1},...,\alpha_{k}\in\Sigma^{\ast}\): \[\begin{array}{lcl} B\shortmid^{x_{1}}...B\shortmid^{x_{k}}B\alpha_{1}...B\alpha_{k} & \overset{\ast}{\vdash} & B\shortmid^{x_{1}}...B\shortmid^{x_{i-1}}B\shortmid^{x_{j}}B\shortmid^{x_{i+1}}...B\shortmid^{x_{k}}B\alpha_{1}...B\alpha_{k}\\ \uparrow & & \uparrow\\ q_{0} & & q_{f} \end{array}\] donde \(q_{0}\) es el estado inicial y \(q_{f}\) es el unico estado final de \(M_{i\leftarrow j}^{\#,k}\). Es claro que la maquina \(M_{i\leftarrow j}^{\#,k}\) simula la instruccion \(\mathrm{N}\bar{\imath}\leftarrow\mathrm{N}\bar{j}\), via la representacion de estados en la cinta con respecto a \(k\).

Para \(1\leq i,j\leq k\), sea \(M_{i\leftarrow j}^{\ast,k}\) una maquina tal que cualesquiera sean \(x_{1},...,x_{k}\in\omega\) y \(\alpha_{1},...,\alpha_{k}\in\Sigma^{\ast}\): \[\begin{array}{lcl} B\shortmid^{x_{1}}...B\shortmid^{x_{k}}B\alpha_{1}...B\alpha_{k} & \overset{\ast}{\vdash} & B\shortmid^{x_{1}}...B\shortmid^{x_{k}}B\alpha_{1}...B\alpha_{i-1}B\alpha_{j}B\alpha_{i+1}...B\alpha_{k}\\ \uparrow & & \uparrow\\ q_{0} & & q_{f} \end{array}\] donde \(q_{0}\) es el estado inicial y \(q_{f}\) es el unico estado final de \(M_{i\leftarrow j}^{\ast,k}\). Es claro que la maquina \(M_{i\leftarrow j}^{\ast,k}\) simula la instruccion \(\mathrm{P}\bar{\imath}\leftarrow\mathrm{P}\bar{j}\), via la representacion de estados en la cinta con respecto a \(k\). La maquina \(M_{i\leftarrow j}^{\ast,k}\), para el caso \(\Sigma=\{a,b\}\) y \(i<j\) puede hacerse de la siguiente manera:

@@figura:figure4.png@@

Para \(1\leq i\leq k\), sea \(M_{i\leftarrow0}^{k}\) una maquina tal que cualesquiera sean \(x_{1},...,x_{k}\in\omega\) y \(\alpha_{1},...,\alpha_{k}\in\Sigma^{\ast}\): \[\begin{array}{lcl} B\shortmid^{x_{1}}...B\shortmid^{x_{k}}B\alpha_{1}...B\alpha_{k} & \overset{\ast}{\vdash} & B\shortmid^{x_{1}}...B\shortmid^{x_{i-1}}BB\shortmid^{x_{i+1}}...B\shortmid^{x_{k}}B\alpha_{1}...B\alpha_{k}\\ \uparrow & & \uparrow\\ q_{0} & & q_{f} \end{array}\] donde \(q_{0}\) es el estado inicial y \(q_{f}\) es el unico estado final de \(M_{i\leftarrow0}^{k}\). Es claro que la maquina \(M_{i\leftarrow0}^{k}\) simula la instruccion \(\mathrm{N}\bar{\imath}\leftarrow0\), via la representacion de estados en la cinta con respecto a \(k\).

Para \(1\leq i\leq k\), sea \(M_{i\leftarrow\varepsilon}^{k}\) una maquina tal que cualesquiera sean \(x_{1},...,x_{k}\in\omega\) y \(\alpha_{1},...,\alpha_{k}\in\Sigma^{\ast}\): \[\begin{array}{lcl} B\shortmid^{x_{1}}...B\shortmid^{x_{k}}B\alpha_{1}...B\alpha_{k} & \overset{\ast}{\vdash} & B\shortmid^{x_{1}}...B\shortmid^{x_{k}}B\alpha_{1}...B\alpha_{i-1}BB\alpha_{i+1}...B\alpha_{k}\\ \uparrow & & \uparrow\\ q_{0} & & q_{f} \end{array}\] donde \(q_{0}\) es el estado inicial y \(q_{f}\) es el unico estado final de \(M_{i\leftarrow\varepsilon}^{k}\). Es claro que la maquina \(M_{i\leftarrow\varepsilon}^{k}\) simula la instruccion \(\mathrm{P}\bar{\imath}\leftarrow\varepsilon\), via la representacion de estados en la cinta con respecto a \(k\).

Sea \[M_{\mathrm{SKIP}}=\left(\{q_{0},q_{f}\},\Gamma,\Sigma,\delta,q_{0},B,\shortmid,\{q_{f}\}\right),\] con \(D_{\delta}=\{(q_{0},B)\}\) y \(\delta(q_{0},B)=(q_{f},B,K)\). Es claro que la maquina \(M_{\mathrm{SKIP}}\) simula la instruccion \(\mathrm{SKIP}\), via la representacion de estados en la cinta con respecto a \(k\) (cualquiera sea el \(k\)).

Para \(1\leq j\leq k\), sea \(IF_{j,k}\) una maquina con estado inicial \(q_{0}\) y dos estados finales \(q_{si}\) y \(q_{no}\) tal que cualesquiera sean \(x_{1},...,x_{k}\in\omega\) y \(\alpha_{1},...,\alpha_{k}\in\Sigma^{\ast}\), si \(x_{j}\neq0\), entonces \[\begin{array}{lcl} B\shortmid^{x_{1}}...B\shortmid^{x_{k}}B\alpha_{1}...B\alpha_{k} & \overset{\ast}{\vdash} & B\shortmid^{x_{1}}...B\shortmid^{x_{k}}B\alpha_{1}...B\alpha_{k}\\ \uparrow & & \uparrow\\ q_{0} & & q_{si} \end{array}\] y si \(x_{j}=0\), entonces \[\begin{array}{lcl} B\shortmid^{x_{1}}...B\shortmid^{x_{k}}B\alpha_{1}...B\alpha_{k} & \overset{\ast}{\vdash} & B\shortmid^{x_{1}}...B\shortmid^{x_{k}}B\alpha_{1}...B\alpha_{k}\\ \uparrow & & \uparrow\\ q_{0} & & q_{no} \end{array}\]

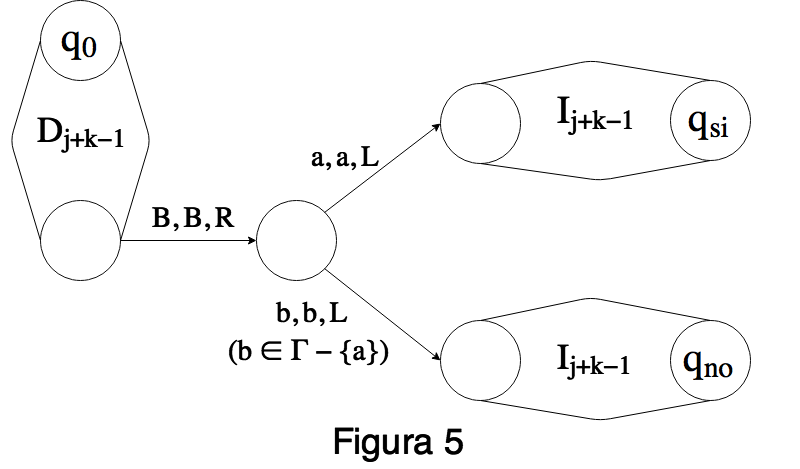
Para \(1\leq i\leq k\) y \(a\in\Sigma\), sea \(IF_{j,k}^{a}\) una maquina con estado inicial \(q_{0}\) y dos estados finales \(q_{si}\) y \(q_{no}\) tal que cualesquiera sean \(x_{1},...,x_{k}\in\omega\) y \(\alpha_{1},...,\alpha_{k}\in\Sigma^{\ast}\), si \(\alpha_{j}\) comienza con \(a\), entonces \[\begin{array}{lcl} B\shortmid^{x_{1}}...B\shortmid^{x_{k}}B\alpha_{1}...B\alpha_{k} & \overset{\ast}{\vdash} & B\shortmid^{x_{1}}...B\shortmid^{x_{k}}B\alpha_{1}...B\alpha_{k}\\ \uparrow & & \uparrow\\ q_{0} & & q_{si} \end{array}\] y en caso contrario \[\begin{array}{lcl} B\shortmid^{x_{1}}...B\shortmid^{x_{k}}B\alpha_{1}...B\alpha_{k} & \overset{\ast}{\vdash} & B\shortmid^{x_{1}}...B\shortmid^{x_{k}}B\alpha_{1}...B\alpha_{k}\\ \uparrow & & \uparrow\\ q_{0} & & q_{no} \end{array}\] La maquina \(IF_{j,k}^{a}\) puede hacerse de la siguinete manera:

@@figura:figure5.png@@

4.4.4.1.2 Ejemplo de maquina simuladora de un programa

A continuacion veremos un ejemplo de como se arma la maquina simuladora de un programa dado. Sea \(\Sigma=\{\blacktriangle,\#\}\) y sea \(\mathcal{P}\) el siguiente programa \[\begin{array}{ll} \mathrm{L}3 & \mathrm{N}4\leftarrow\mathrm{N}4+1\\ & \mathrm{P}1\leftarrow\ ^{\curvearrowright}\mathrm{P}1\\ & \mathrm{IF\ P}1\ \mathrm{BEGINS\ }\blacktriangle\ \mathrm{GOTO}\;\mathrm{L}3\\ & \mathrm{P}3\leftarrow\mathrm{P}3.\# \end{array}\] Tomemos \(k=5\). Es claro que \(k\geq N(\mathcal{P})=4\). A la maquina que simulara a \(\mathcal{P}\) respecto de \(k\), la llamaremos \(M_{sim}\) y sera la siguiente maquina:

@@figura:figure6.png@@

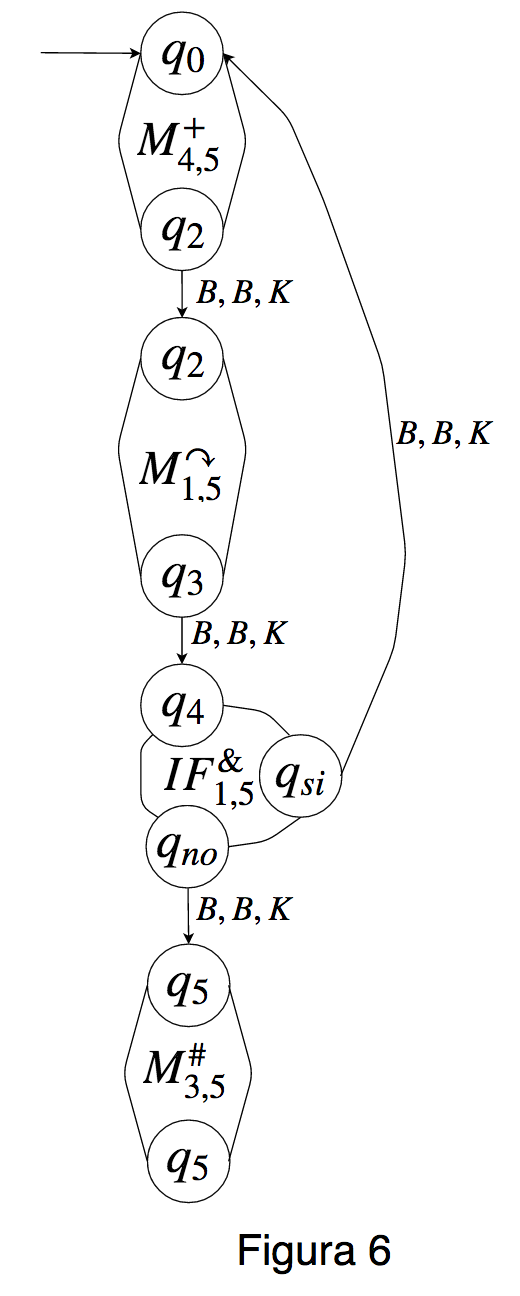
Veamos con un ejemplo como \(M_{sim}\) simula a \(\mathcal{P}\). Supongamos que corremos \(\mathcal{P}\) desde el estado \[\left\Vert 2,1,0,5,3,\#\blacktriangle\#\#,\varepsilon,\blacktriangle\blacktriangle,\#\blacktriangle,\#\right\Vert\] Tendremos entonces la siguiente sucesion de descripciones instantaneas: \[\begin{aligned} & (1,\left\Vert 2,1,0,5,3,\#\blacktriangle\#\#,\varepsilon,\blacktriangle\blacktriangle,\#\blacktriangle,\#\right\Vert )\\ \\ & (2,\left\Vert 2,1,0,6,3,\#\blacktriangle\#\#,\varepsilon,\blacktriangle\blacktriangle,\#\blacktriangle,\#\right\Vert )\\ \\ & (3,\left\Vert 2,1,0,6,3,\blacktriangle\#\#,\varepsilon,\blacktriangle\blacktriangle,\#\blacktriangle,\#\right\Vert )\\ \\ & (1,\left\Vert 2,1,0,6,3,\blacktriangle\#\#,\varepsilon,\blacktriangle\blacktriangle,\#\blacktriangle,\#\right\Vert )\\ \\ & (2,\left\Vert 2,1,0,7,3,\blacktriangle\#\#,\varepsilon,\blacktriangle\blacktriangle,\#\blacktriangle,\#\right\Vert )\\ \\ & (3,\left\Vert 2,1,0,7,3,\#\#,\varepsilon,\blacktriangle\blacktriangle,\#\blacktriangle,\#\right\Vert )\\ \\ & (4,\left\Vert 2,1,0,7,3,\#\#,\varepsilon,\blacktriangle\blacktriangle,\#\blacktriangle,\#\right\Vert )\\ \\ & (5,\left\Vert 2,1,0,7,3,\#\#,\varepsilon,\blacktriangle\blacktriangle\#,\#\blacktriangle,\#\right\Vert ) \end{aligned}\] Si hacemos funcionar a \(M_{sim}\) desde \(q_{0}B\shortmid^{2}B\shortmid BB\shortmid^{5}B\shortmid^{3}B\#\blacktriangle\#\#BB\blacktriangle\blacktriangle B\#\blacktriangle B\#B\) obtendremos una sucesion de descripciones instantaneas dentro de la cual estara la siguiente subsucesion que se corresponde con las descripciones instantaneas de la computacion anterior. \[\begin{aligned} q_{0}B & \shortmid^{2}B\shortmid BB\shortmid^{5}B\shortmid^{3}B\#\blacktriangle\#\#BB\blacktriangle\blacktriangle B\#\blacktriangle B\#B\\ \\q_{1}B & \shortmid^{2}B\shortmid BB\shortmid^{6}B\shortmid^{3}B\#\blacktriangle\#\#BB\blacktriangle\blacktriangle B\#\blacktriangle B\#B\\ q_{2}B & \shortmid^{2}B\shortmid BB\shortmid^{6}B\shortmid^{3}B\#\blacktriangle\#\#BB\blacktriangle\blacktriangle B\#\blacktriangle B\#B\\ \\q_{3}B & \shortmid^{2}B\shortmid BB\shortmid^{6}B\shortmid^{3}B\blacktriangle\#\#BB\blacktriangle\blacktriangle B\#\blacktriangle B\#B\\ q_{4}B & \shortmid^{2}B\shortmid BB\shortmid^{6}B\shortmid^{3}B\blacktriangle\#\#BB\blacktriangle\blacktriangle B\#\blacktriangle B\#B\\ \\q_{si}B & \shortmid^{2}B\shortmid BB\shortmid^{6}B\shortmid^{3}B\blacktriangle\#\#BB\blacktriangle\blacktriangle B\#\blacktriangle B\#B\\ q_{0}B & \shortmid^{2}B\shortmid BB\shortmid^{6}B\shortmid^{3}B\blacktriangle\#\#BB\blacktriangle\blacktriangle B\#\blacktriangle B\#B\\ \\q_{1}B & \shortmid^{2}B\shortmid BB\shortmid^{7}B\shortmid^{3}B\blacktriangle\#\#BB\blacktriangle\blacktriangle B\#\blacktriangle B\#B\\ q_{2}B & \shortmid^{2}B\shortmid BB\shortmid^{7}B\shortmid^{3}B\blacktriangle\#\#BB\blacktriangle\blacktriangle B\#\blacktriangle B\#B\\ \\q_{3}B & \shortmid^{2}B\shortmid BB\shortmid^{7}B\shortmid^{3}B\#\#BB\blacktriangle\blacktriangle B\#\blacktriangle B\#B\\ q_{4}B & \shortmid^{2}B\shortmid BB\shortmid^{7}B\shortmid^{3}B\#\#BB\blacktriangle\blacktriangle B\#\blacktriangle B\#B\\ \\q_{no}B & \shortmid^{2}B\shortmid BB\shortmid^{7}B\shortmid^{3}B\#\#BB\blacktriangle\blacktriangle B\#\blacktriangle B\#B\\ q_{5}B & \shortmid^{2}B\shortmid BB\shortmid^{7}B\shortmid^{3}B\#\#BB\blacktriangle\blacktriangle B\#\blacktriangle B\#B\\ \\q_{6}B & \shortmid^{2}B\shortmid BB\shortmid^{7}B\shortmid^{3}B\#\#BB\blacktriangle\blacktriangle\#B\#\blacktriangle B\#B \end{aligned}\] Dejamos al lector ver en detalle el paralelismo que hay entre las dos sucesiones de descripciones instantaneas arriba expuestas.

4.4.4.1.3 La contruccion de la maquina simuladora

A continuacion describiremos en general como hacer la maquina simuladora de \(\mathcal{P}\), respecto de \(k\). Supongamos que \(\mathcal{P}=I_{1}...I_{n}\). Para cada \(i=1,...,n\), llamaremos \(M_{i}\) a la maquina que simulara el efecto que produce la instruccion \(I_{i}\), es decir tomemos

1. adhocprefix-adhocsufix \(M_{i}=M_{j,k}^{+}\), si \(Bas(I_{i})=\mathrm{N}\bar{j}\leftarrow\mathrm{N}\bar{j}+1\)

2. adhocprefix-adhocsufix \(M_{i}=M_{j,k}^{\dot{-}}\), si \(Bas(I_{i})=\mathrm{N}\bar{j}\leftarrow\mathrm{N}\bar{j}\dot{-}1\)

3. adhocprefix-adhocsufix \(M_{i}=M_{j,k}^{a}\), si \(Bas(I_{i})=\mathrm{P}\bar{j}\leftarrow\mathrm{P}\bar{j}.a\)

4. adhocprefix-adhocsufix \(M_{i}=M_{j,k}^{\curvearrowright}\), si \(Bas(I_{i})=\mathrm{P}\bar{j}\leftarrow\ ^{\curvearrowright}\mathrm{P}\bar{j}\)

5. adhocprefix-adhocsufix \(M_{i}=M_{j\leftarrow m}^{\#,k}\), si \(Bas(I_{i})=\mathrm{N}\bar{j}\leftarrow\mathrm{N}\bar{m}\)

6. adhocprefix-adhocsufix \(M_{i}=M_{j\leftarrow m}^{\ast,k}\), si \(Bas(I_{i})=\mathrm{P}\bar{j}\leftarrow\mathrm{P}\bar{m}\)

7. adhocprefix-adhocsufix \(M_{i}=M_{j\leftarrow0}^{k}\), si \(Bas(I_{i})=\mathrm{N}\bar{j}\leftarrow0\)

8. adhocprefix-adhocsufix \(M_{i}=M_{j\leftarrow\varepsilon}^{k}\), si \(Bas(I_{i})=\mathrm{P}\bar{j}\leftarrow\varepsilon\)

9. adhocprefix-adhocsufix \(M_{i}=M_{\mathrm{SKIP}}\), si \(Bas(I_{i})=\mathrm{SKIP}\)

10. adhocprefix-adhocsufix \(M_{i}=IF_{j,k}\), si \(Bas(I_{i})=\mathrm{IF}\;\mathrm{N}\bar{j}\not=0\) \(\mathrm{GOTO}\;\mathrm{L}\bar{m}\), para algun \(m\)

11. adhocprefix-adhocsufix \(M_{i}=IF_{j,k}^{a}\), si \(Bas(I_{i})=\mathrm{IF}\;\mathrm{P}\bar{j}\;\mathrm{BEGINS}\;a\;\mathrm{GOTO}\;\mathrm{L}\bar{m}\), para algun \(m\)

Ya que la maquina \(M_{i}\) puede tener uno o dos estados finales, la representaremos como se muestra a continuacion:

@@figura:figure7.png@@

entendiendo que en el caso en que \(M_{i}\) tiene un solo estado final, este esta representado por el circulo de abajo a la izquierda y en el caso en que \(M_{i}\) tiene dos estados finales, el circulo de abajo a la izquierda corresponde al estado final \(q_{no}\) y el circulo de abajo a la derecha corresponde al estado \(q_{si}\). Para armar la maquina que simulara a \(\mathcal{P}\) hacemos lo siguiente. Primero unimos las maquinas \(M_{1},...,M_{n}\) de la siguiente manera:

@@figura:figure8.png@@

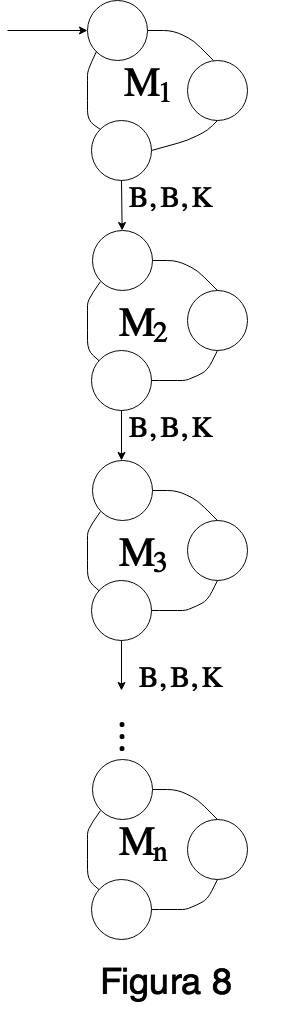
Luego para cada \(i\) tal que \(Bas(I_{i})\) es de la forma \(\alpha\mathrm{GOTO}\;\mathrm{L}\bar{m}\), ligamos con una flecha de la forma \[\underrightarrow{\;\;\;\;\;\;B,B,K\;\;\;\;\;\;}\] el estado final \(q_{si}\) de la \(M_{i}\) con el estado inicial de la \(M_{h}\), donde \(h\) es tal que \(I_{h}\) es la primer instruccion que tiene label \(\mathrm{L}\bar{m}\).

4.4.4.2 El lema de la simulacion

A continuacion enunciaremos en forma de lema la existencia de la maquina simuladora y de las propiedades esenciales que usaremos luego para probar que toda funcion \(\Sigma\)-computable es \(\Sigma\)-Turing computable.

Cabe destacar que si bien la veracidad de este lema es sustentada en las explicaciones anteriores, una prueba formal rigurosa del mismo resultaria extremadamente larga y tediosa. La ventaja de que sea un resultado intuitivamente claro nos permite aceptarlo y seguir adelante en nuestro analisis.

4.4.4.3 Turing vence a Neumann

En lo que sigue usaremos la existencia de la maquina simuladora de un programa para probar que toda funcion \(\Sigma\)-computable es \(\Sigma\)-Turing computable. Antes un lema.

Proof. Sea \(\mathcal{P}\) un programa que compute a \(f\). Sea \(r\in\mathbf{N}\) tal que \(r>N(\mathcal{P}),n,m\). Sea \(\mathcal{\tilde{P}}\) el resultado de reemplazar en \(\mathcal{P}\) cada instruccion de la forma \[\alpha\mathrm{GOTO}\;\mathrm{L}\bar{\imath}\] con \(\alpha\in\{\varepsilon\}\cup\{\mathrm{L}\bar{j}:j\in\mathbf{N}\}\) por \(\alpha\mathrm{IF\ N}\bar{r}\neq0\ \mathrm{GOTO}\;\mathrm{L}\bar{\imath}\). Ahora sea \(\mathcal{Q}\) el siguiente programa \[\begin{array}{l} \mathrm{N}\bar{r}\leftarrow\mathrm{N}\bar{r}+1\\ \mathcal{\tilde{P}}\\ \mathrm{N}1\leftarrow0\\ \vdots\\ \mathrm{N}\bar{r}\leftarrow0\\ \mathrm{P}2\leftarrow\varepsilon\\ \vdots\\ \mathrm{P}\bar{r}\leftarrow\varepsilon \end{array}\] Es facil ver que \(\mathcal{Q}\) tiene las propiedades (1) y (2).  

Por supuesto, hay un lema analogo para el caso en que \(f\) llega a \(\omega\) en lugar de llegar a \(\Sigma^{\ast}\). Ahora si, el anunciado teorema:

Proof. Supongamos \(O=\Sigma^{\ast}\). Por el Lema 4.54 existe \(\mathcal{P}\in\mathrm{Pro}^{\Sigma}\) el cual computa \(f\) y tiene las propiedades (1) y (2). Sea \(k=\max\{n,m,N(\mathcal{P})\}\) y sea \(M_{sim}\) la maquina de Turing con unit que simula a \(\mathcal{P}\) respecto de \(k\). Como puede observarse, la maquina \(M_{sim}\), no necesariamente computara a \(f\). Sea \(M_{1}\) la siguiente maquina:

@@figura:figure9.png@@

(Cuando \(n=0\) debemos interpretar que \(D_{0}=\left(\{q_{0},q_{f}\},\Gamma,\Sigma,\delta,q_{0},B,\shortmid,\{q_{f}\}\right)\), con \(D_{\delta}=\{(q_{0},B)\}\) y \(\delta(q_{0},B)=(q_{f},B,K)\). Notese que \(M_{1}\) cumple que para cada \((\vec{x},\vec{\alpha})\in\omega^{n}\times\Sigma^{\ast m}\), \[\left\lfloor q_{0}B\shortmid^{x_{1}}B...B\shortmid^{x_{n}}B\alpha_{1}B...B\alpha_{m}B\right\rfloor \overset{\ast}{\vdash}\left\lfloor q_{f}B\shortmid^{x_{1}}B...B\shortmid^{x_{n}}B^{k-n}B\alpha_{1}B...B\alpha_{m}B\right\rfloor\] Sea \(M_{2}\) la siguiente maquina

@@figura:figure10.png@@

Notese que \(M_{2}\) cumple que para cada \(\alpha\in\Sigma^{\ast}\), \[\left\lfloor q_{0}B^{k+1}\alpha\right\rfloor \overset{\ast}{\vdash}\left\lfloor q_{f}B\alpha\right\rfloor\] Sea \(M\) la siguiente maquina:

@@figura:figure11.png@@

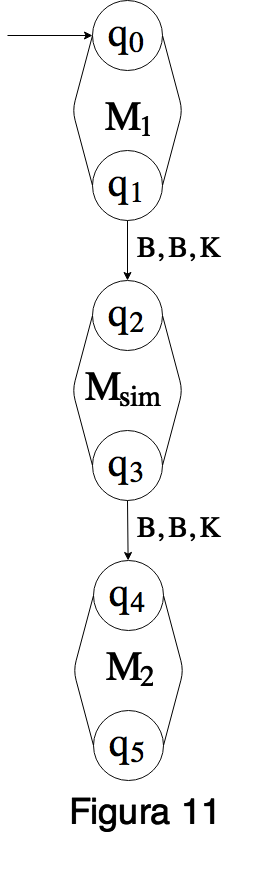
A continuacion veremos que \(M\) computa a \(f\). Supongamos que \((\vec{x},\vec{\alpha})\in(\omega^{n}\times\Sigma^{\ast m})-D_{f}\). Deberemos ver que \(M\) no termina partiendo de

\(\left\lfloor q_{0}B\shortmid^{x_{1}}B...B\shortmid^{x_{n}}B\alpha_{1}B...B\alpha_{m}B\right\rfloor\)

Primero notemos que, ya que \(\mathcal{P}\) computa a \(f\), tenemos que \(\mathcal{P}\) no termina partiendo de \(\left\Vert x_{1},...,x_{n},\alpha_{1},...,\alpha_{m}\right\Vert\) por lo cual \(\mathcal{P}\) no termina partiendo de \[\left\Vert x_{1},...,x_{n},\overset{k-n}{\overbrace{0,...,0}},\alpha_{1},...,\alpha_{m},\overset{k-m}{\overbrace{\varepsilon,...,\varepsilon}}\right\Vert\] lo cual implica (Lema 4.53) que

\(M_{sim}\) no termina partiendo de \(\left\lfloor q_{0}B\shortmid^{x_{1}}B...B\shortmid^{x_{n}}B^{k-n}B\alpha_{1}B...B\alpha_{m}B\right\rfloor\)

Ahora notese que si hacemos funcionar a \(M\) desde la descripcion instantanea dada en (*), llegaremos (via la copia de \(M_{1}\) dentro de \(M\)) indefectiblemente (ya que \(M\) es deterministica) a la siguiente descripcion instantanea \[\left\lfloor q_{2}B\shortmid^{x_{1}}B...B\shortmid^{x_{n}}B^{k-n}B\alpha_{1}B...B\alpha_{m}B\right\rfloor\] Luego entonces (**) nos dice que al seguir trabajando \(M\) (ahora via la copia de \(M_{sim}\) dentro de \(M\)), la maquina \(M\) nunca terminara.

Para terminar de ver que \(M\) computa a \(f\), tomemos \((\vec{x},\vec{\alpha})\in D_{f}\) y veamos que \[\left\lfloor q_{0}B\shortmid^{x_{1}}B...B\shortmid^{x_{n}}B\alpha_{1}B...B\alpha_{m}B\right\rfloor \overset{\ast}{\underset{M}{\vdash}}\left\lfloor q_{5}Bf(\vec{x},\vec{\alpha})\right\rfloor\] y que la maquina \(M\) se detiene en \(\left\lfloor q_{5}Bf(\vec{x},\vec{\alpha})\right\rfloor\). La maquina \(M\) se detiene en \(\left\lfloor q_{5}Bf(\vec{x},\vec{\alpha})\right\rfloor\) ya que \(q_{5}\) es el estado final de una copia de \(M_{2}\) y por lo tanto no sale ninguna flecha desde el. Ya que \(\mathcal{P}\) computa a \(f\) y tiene la propiedad (2) del Lema 4.54, tenemos que \(\mathcal{P}\) termina partiendo de \(\left\Vert x_{1},...,x_{n},\alpha_{1},...,\alpha_{m}\right\Vert\) y llega al estado \(\left\Vert f(\vec{x},\vec{\alpha})\right\Vert\), o lo que es lo mismo, \(\mathcal{P}\) termina partiendo de \[\left\Vert x_{1},...,x_{n},\overset{k-n}{\overbrace{0,...,0}},\alpha_{1},...,\alpha_{m},\overset{k-m}{\overbrace{\varepsilon,...,\varepsilon}}\right\Vert\] y llega al estado \[\left\Vert \overset{k}{\overbrace{0,...,0}},f(\vec{x},\vec{\alpha}),\overset{k-1}{\overbrace{\varepsilon,...,\varepsilon}}\right\Vert\] Pero entonces el Lema 4.53 nos dice que

1. adhocprefix(***)adhocsufix \(\left\lfloor q_{0}B\shortmid^{x_{1}}B...B\shortmid^{x_{n}}B^{k-n}B\alpha_{1}B...B\alpha_{m}B\right\rfloor \overset{\ast}{\underset{M_{sim}}{\vdash}}\left\lfloor q_{f}B^{k+1}f(\vec{x},\vec{\alpha})\right\rfloor\)

Como ya lo vimos, si hacemos funcionar a \(M\) desde \(\left\lfloor q_{0}B\shortmid^{x_{1}}B...B\shortmid^{x_{n}}B\alpha_{1}B...B\alpha_{m}B\right\rfloor\), llegaremos (via la copia de \(M_{1}\) dentro de \(M\)) indefectiblemente a la siguiente descripcion instantanea \[\left\lfloor q_{2}B\shortmid^{x_{1}}B...B\shortmid^{x_{n}}B^{k-n}B\alpha_{1}B...B\alpha_{m}B\right\rfloor\] Luego (***) nos dice que, via la copia de \(M_{sim}\) dentro de \(M\), llegaremos a \(\left\lfloor q_{3}B^{k+1}f(\vec{x},\vec{\alpha})\right\rfloor\) e inmediatamente a \(\left\lfloor q_{4}B^{k+1}f(\vec{x},\vec{\alpha})\right\rfloor\). Finalmente, via la copia de \(M_{2}\) dentro de \(M\), llegaremos a \(\left\lfloor q_{5}Bf(\vec{x},\vec{\alpha})\right\rfloor\), lo cual termina de demostrar que \(M\) computa a \(f\)